Digital surveillance systems for climate-sensitive diseases
Paula Moraga, Ph.D.
Assistant Professor of Statistics
King Abdullah University of Science
and Technology (KAUST), Saudi Arabia


Books
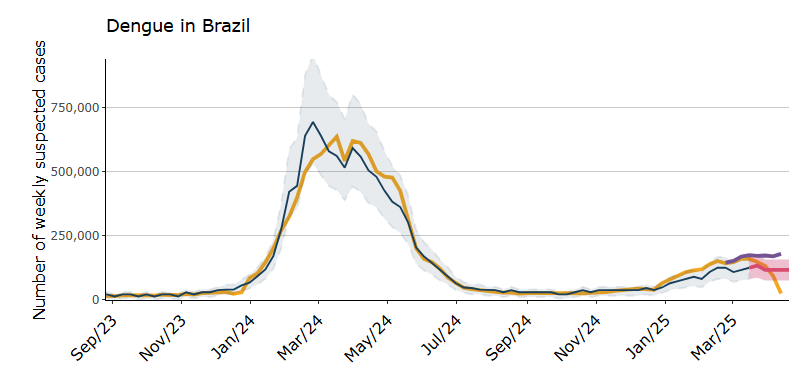
Dengue emergency 2024
2024 has been the worst year for dengue cases on record, with over 10 million cases reported globally. Brazil one of the most affected countries
Mosquito-borne diseases
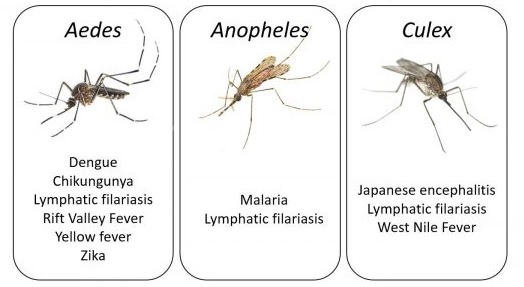
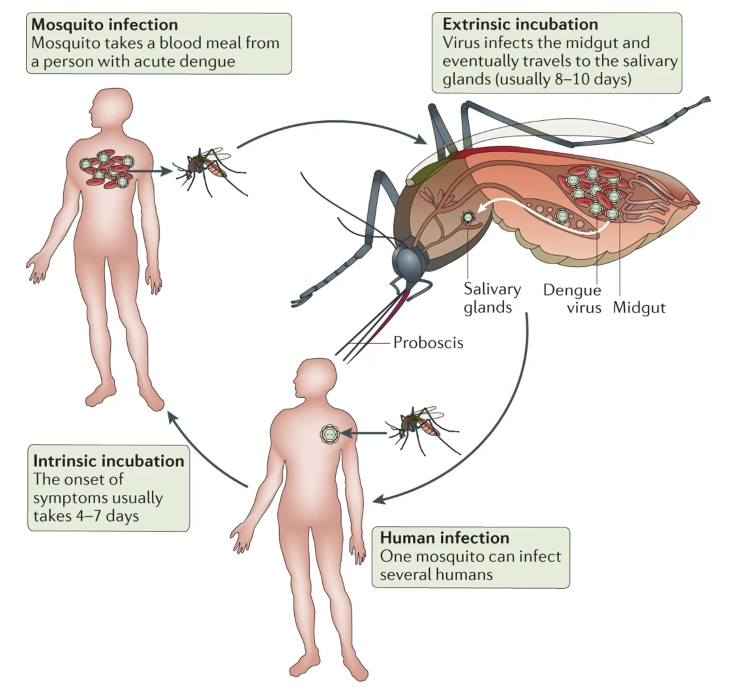
Diseases spread because when a mosquito bites an infected person it also swallows any viruses or parasites living in the blood of the infected person, and these can be transferred to the next person the mosquito bites
Mosquito-borne diseases
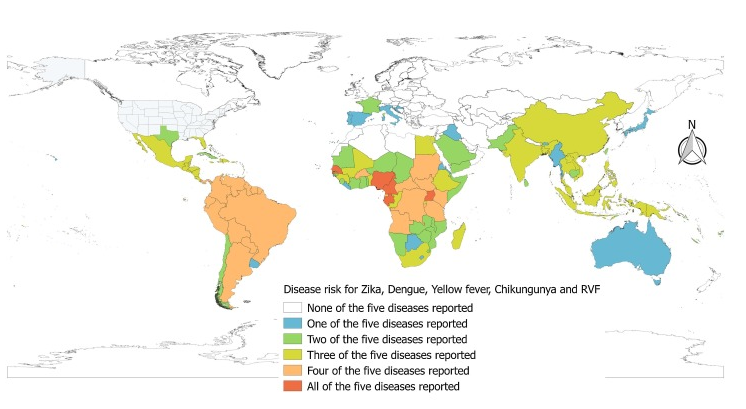
Leta et al., International Journal of Infectious Diseases, 2018
Why are diseases spreading?
Rapid and unplanned urbanization and deforestation
Climate change
Global travel
What can we do to prevent the spread of infectious diseases?
Need to acknowledge connectivity between people, animals, and their shared environment and work together to prevent disease outbreaks and save lives
Access to healthcare
and education

Vaccine development and mosquito control

Early warning and response systems

Disease surveillance systems
Overview of my research to help inform disease surveillance
- Use of digital data for nowcasting dengue in Brazil
- Development of spatial deep learning methods for dengue forecasting
- Translation of research into action to inform policymaking
Disease surveillance systems
Disease surveillance systems
Disease surveillance systems are critical to early detection of epidemics and the design of control strategies
Traditional surveillance systems rely on data gathered with a considerable delay and make surveillance systems ineffective for real-time surveillance



Digital data sources
Real-time digital information may enable to detect outbreaks earlier

“Flu plus fever, not a good way to start the weekend”
“I’m so irritated at this cough and fever”
“This flu, fever & throat ache won’t let me sleep”
Demographic and environmental risk factors

Digital health surveillance system
- Data-gathering platform
- Modelling framework that integrates multiple data sources so as to produce local probabilistic predictions of disease activity in real-time
- Interactive dashboard that alerts public health officials when elevated disease levels are anticipated, and provides insights about disease drivers

Dengue surveillance in Brazil
Dengue emergency 2024
2024 has been the worst year for dengue cases on record, with over 10 million cases reported globally. Brazil one of the most affected countries
Dengue in Brazil
Dengue is a disease transmitted by mosquitoes of the Aedes species that poses significant public health challenges in tropical and sub-tropical regions, including Brazil.
Many dengue cases only result in mild, flu-like illness, but some can be severe and even fatal.
Dengue does not have a specific treatment, but early detection and timely access to proper medical care significantly reduce the fatality rates associated with severe cases. Prevention focuses on personal protection and mosquito control.
Surveillance systems are crucial for dengue prevention and control.
 Aedes aegypti
Aedes aegypti
 Vector control efforts
Vector control efforts
Reporting delays in official dengue cases
In Brazil, the InfoDengue system collects and generates indicators of dengue and other arboviruses: https://info.dengue.mat.br/
In principle, dengue is meant to be reported within seven days of case identification. In practice,
- Less than 50% cases are reported within one week
- Less than 75% cases reported within four weeks
- No more than 90% cases reported within nine weeks
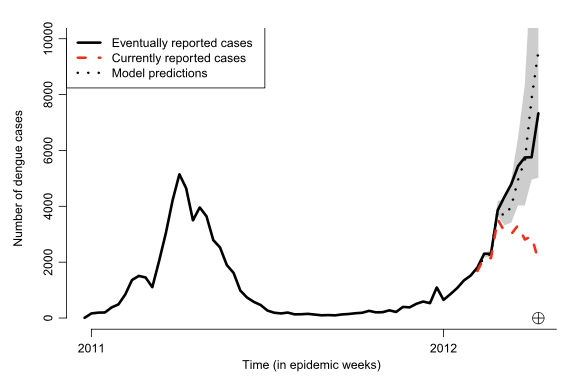
Reported dengue cases in Rio de Janeiro, January 2011 to April 2012. Red line reported cases for those weeks.
Black line eventually reported cases after 10 weeks.
Aim: improving dengue nowcasting in Brazil using real-time search query data
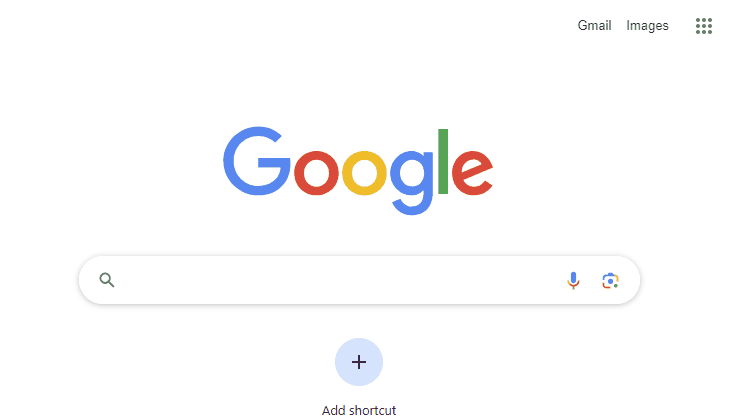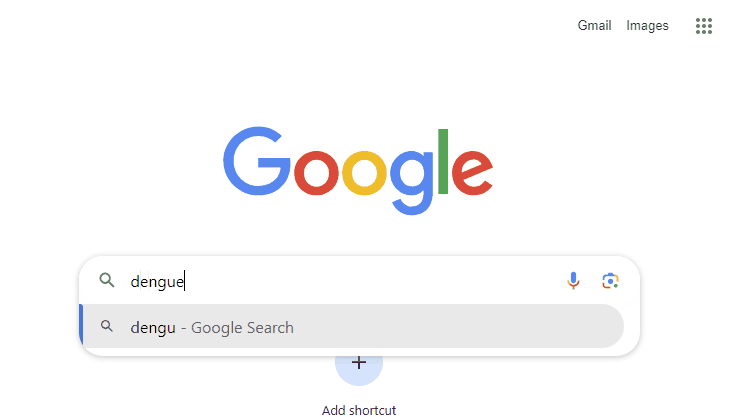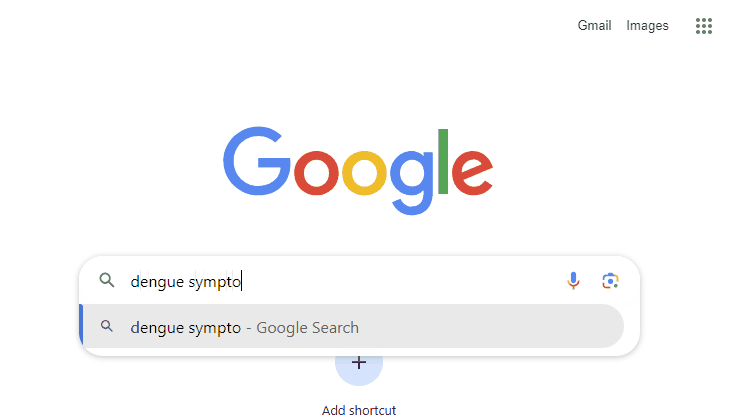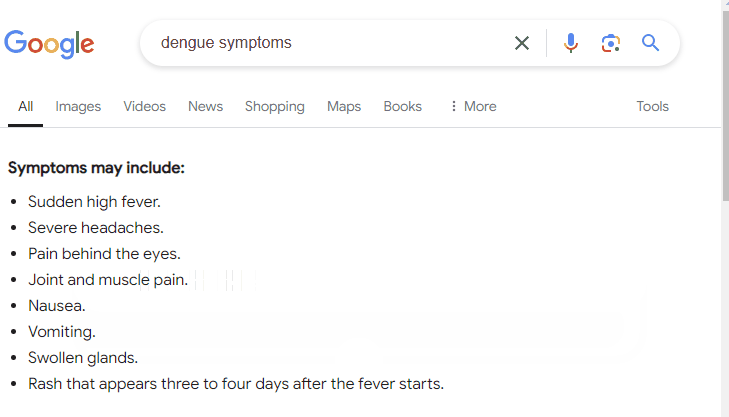
Google Trends data
Google Trends index for a specific keyword is an index ranging from 0 to 100. Calculated using the number of searches for that keyword divided by the total number of searches of the region and time period considered to compare relative popularity.
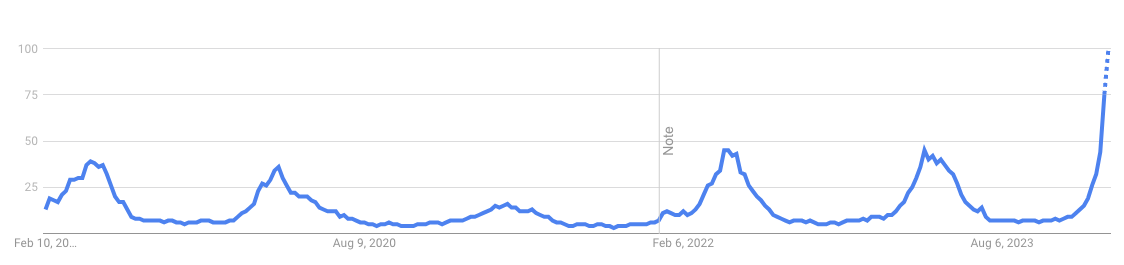
Weekly Google Trends index for keyword ‘dengue’ in Brazil, 2019 to 2024.
Dengue nowcasting in Brazil
We wish to assess the value of Google Trends for weekly dengue nowcasting in the 27 Brazilian states using dengue data from March to June 2024.
Each we collect reported dengue cases and Google Trends indices, fit several nowcasting models using different information, and compare nowcasts with the actual cases reported after 10 weeks. Models incorporate:
- Only dengue cases
- Only Google Trends data
- Both cases and Google Trends
- Joint model for reported cases and delay distribution by InfoDengue
- Naive approach where nowcasts are reported cases in previous week
Performance evaluated using error measures and uncertainty intervals
Selecting keywords for Google Trends indices
Correlation among dengue cases and Google Trends indices for several dengue-related keywords in Brazil, Jan 2013 - Dec 2023
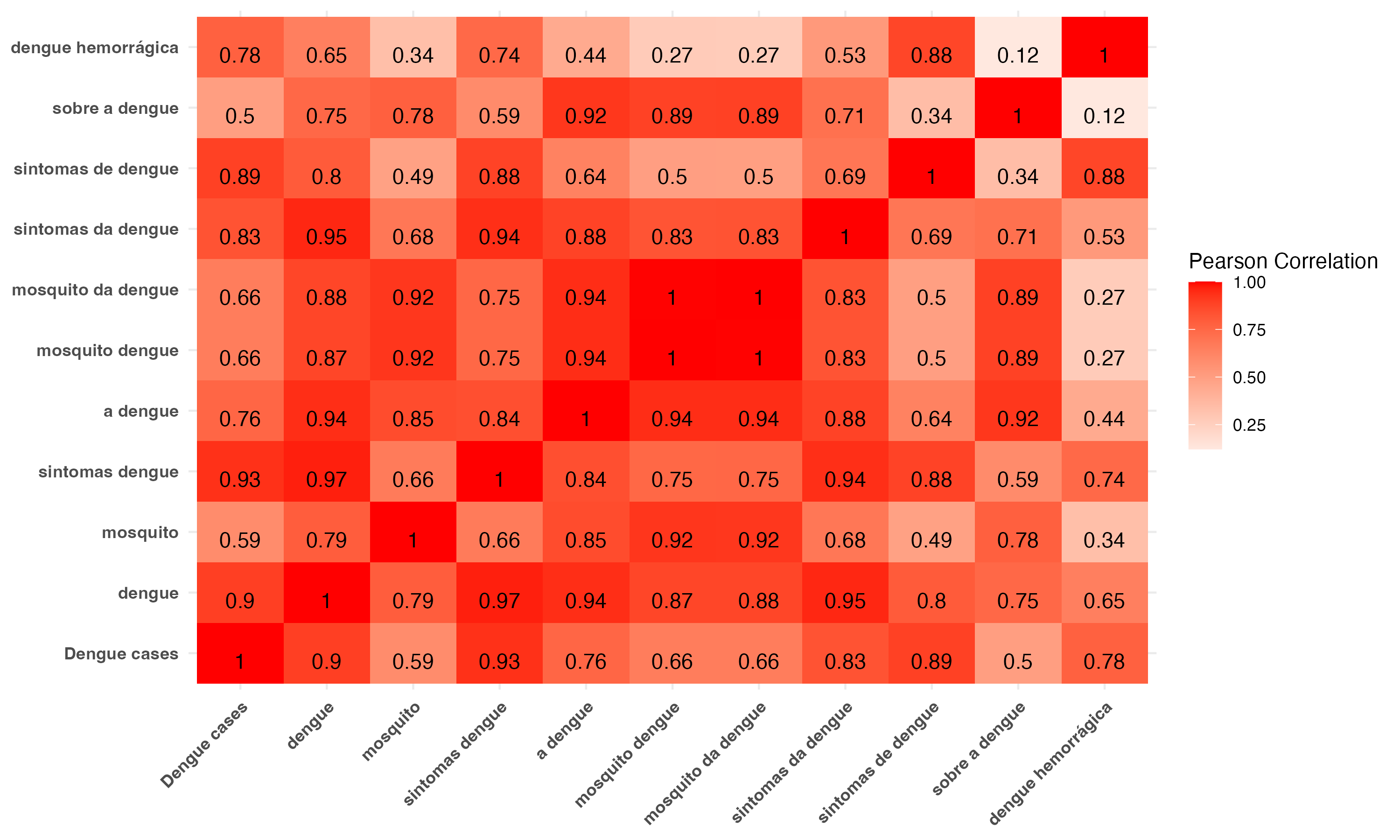
We incorporate Google Trends indices for keywords sintomas dengue and dengue
Highest correlation between dengue cases and keywords sintomas dengue (0.93), dengue (0.90), and sintomas de dengue (0.89). Highest intercorrelations among keywords sintomas dengue and dengue (0.97)
Google Keyword Planner to find keywords related to dengue in Brazil Jan - Apr 2024. High search interest in dengue and sintomas de dengue
Nowcasts obtained using models with moving window strategy
\(y_t\) cases reported in InfoDengue in week \(t\), \(c_t\) actual cases reported 10 weeks after \(t\). \(y_t\) \(<\) \(c_t\) due to reporting delays. Nowcasts \(\hat c_t\) obtained for each week March 3 to June 2, 2024 using models trained on data from past three years excluding four most recent weeks to balance maintaining recent information with discarding incomplete data (less 75% cases reported within four weeks)
- Model DCases SARIMA Seasonal Autoregressive Integrated Moving-Average
- Model DCGT. SARIMAX SARIMA with eXogenous factors (GT indices)
- Model GT. Linear model \(E[y_t]=\beta_0 + \beta_1\ {\mbox{GT1}}_{t} + \beta_2\ {\mbox{GT2}}_{t}\)
- Model InfoDengue. Joint model for reported cases and delay distribution
- Naive baseline. Nowcast is cases reported in the previous week: \(\hat{c}_t = y_{t-1}\)
Nowcasts \(\hat c_t\) compared with actual number of cases \(c_t\) using error and uncertainty measures
Results
Results vary by state. In general, Google Trends and joint model for reported cases and delay distribution by InfoDengue are the best-performing approaches
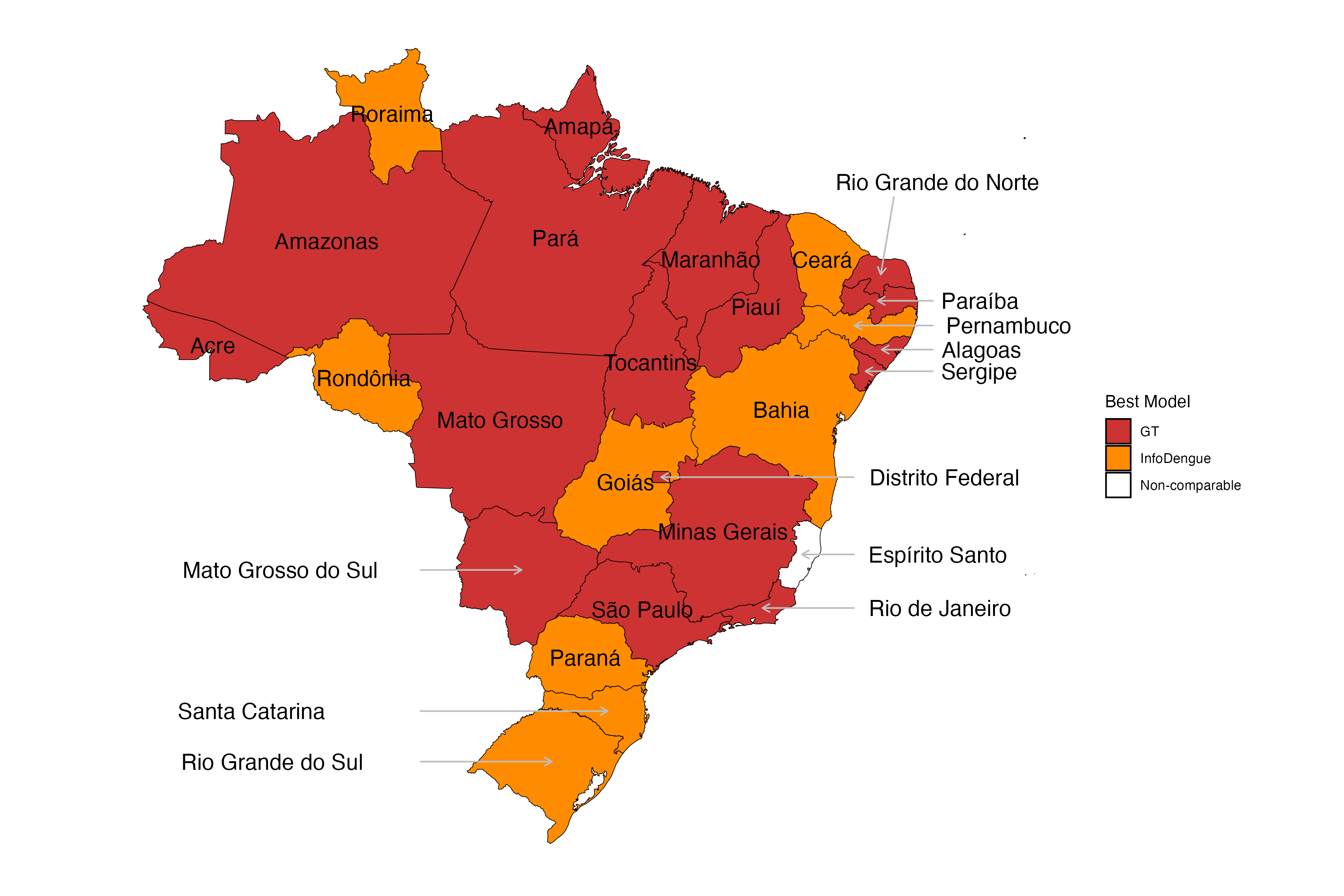

Weekly dengue nowcasts March to June, 2024
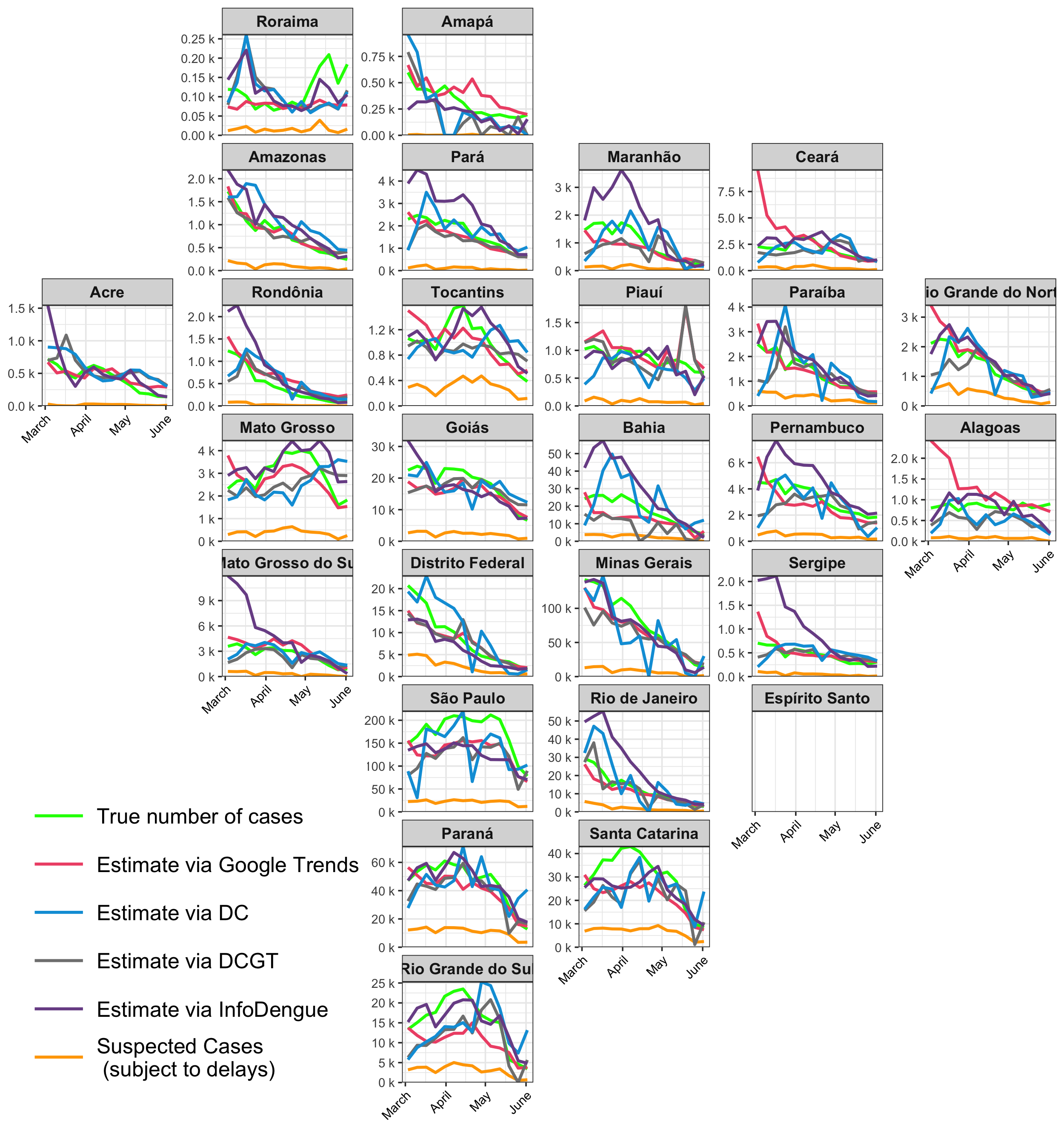
Weekly dengue nowcasts in Rio de Janeiro, March to June, 2024
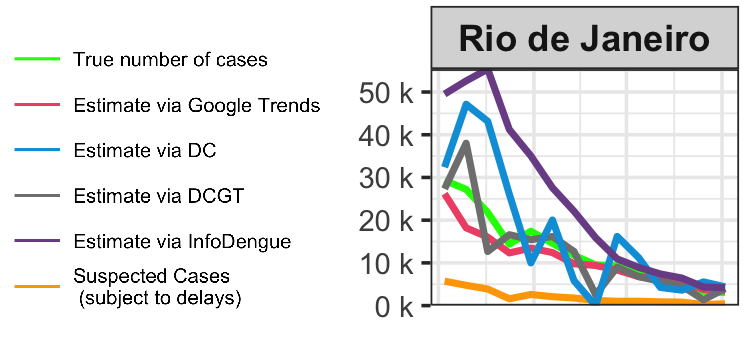
Dengue tracker in Brazil
Dengue-tracker provides weekly updates on the number of dengue cases per state in Brazil
We present official and corrected case counts incorporating information from Google Trends
Reports assist policymakers
and the general public in understanding dengue levels
and guide their decisions
![]()
Dengue tracker in Brazil
Dengue tracker in Brazil
Impact Dengue-tracker
- Dengue-tracker has been used to inform the Brazilian Ministry of Health
- Several weeks official dengue cases were not reported and the model from InfoDengue did not produce nowcasts. Nowcasts by Dengue-tracker were crucial to keep the Ministry of Health informed
- Espirito Santo state stopped reporting cases, and Dengue-tracker was the only source of information about dengue activity levels in the state
- Dengue-tracker disseminated in social media and among contacts. General population used Dengue-tracker to be more informed about dengue situation
![]()
Forecasting
Disease forecasting
Nowcasting methods allow us to understand disease activity levels in real-time and make better informed decisions
It is also important to advance forecasting methods to predict the number of cases that will occur in the future so we have more time to be prepared and allocate resources in areas of greatest need to reduce disease impacts
Disease forecasting
Forecasting methods for dengue and other mosquito-borne diseases can improve their accuracy by including risk factors such as climate and environmental variables
Traditional forecasting methods fail to integrate the complex relationships between disease and risk factors

We developed a forecasting method that addresses these limitations and allows us to more accurately predict future disease cases to better inform policymaking
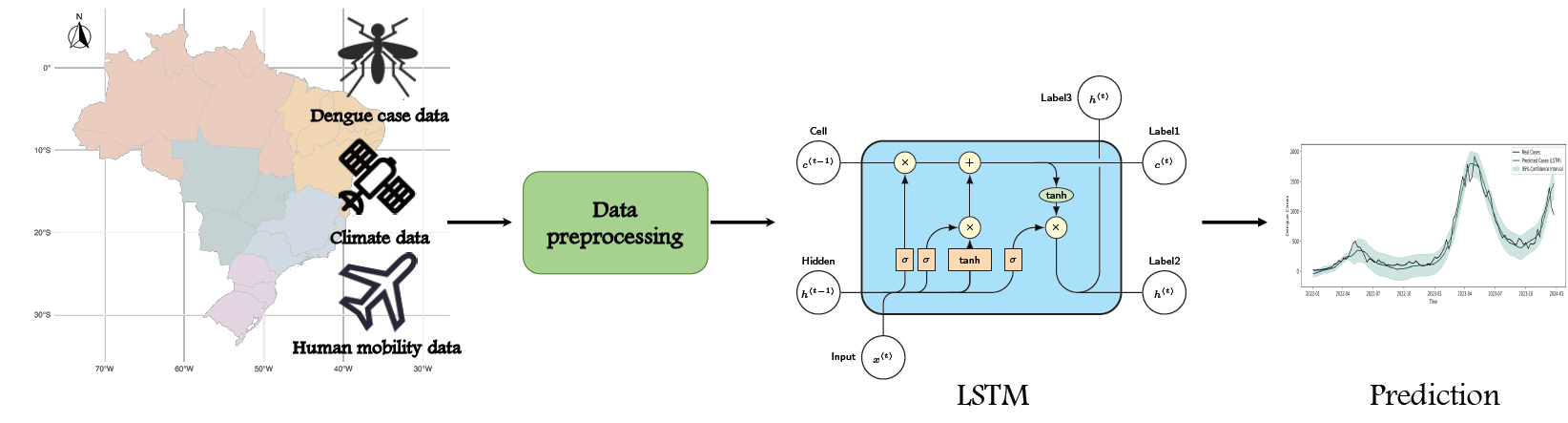
Forecasting with Spatial Deep Learning
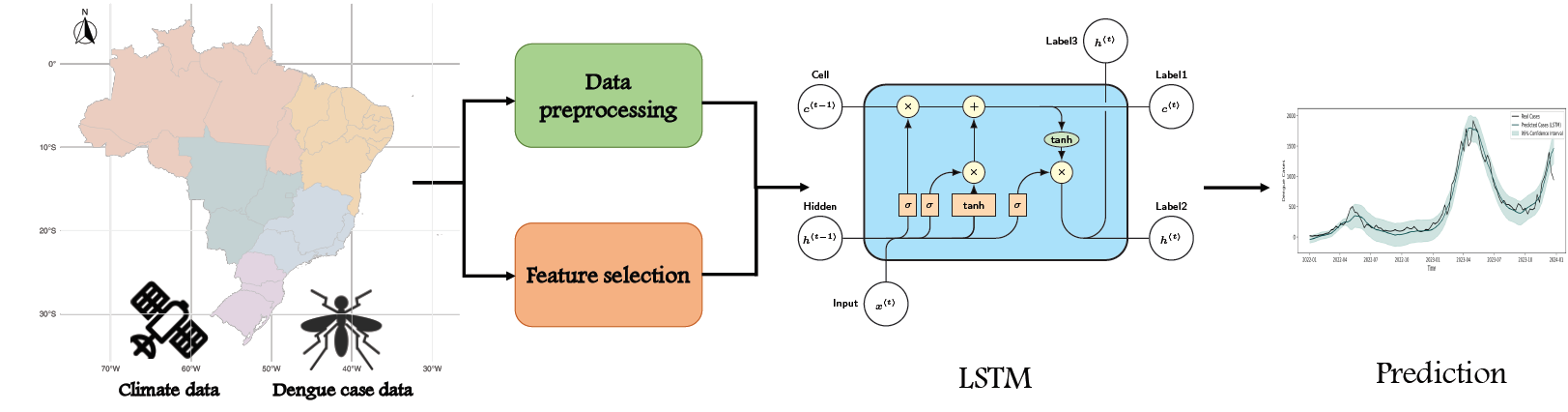
We developed a Long Short-Term Memory (LSTM)-based model that accounts for delayed and non-linear effects of climate and environmental variables, and spatial information for dengue forecasting to provide improved predictions
Dengue data
Assessed LSTM model by forecasting dengue 4 and 12 weeks ahead in Brazil
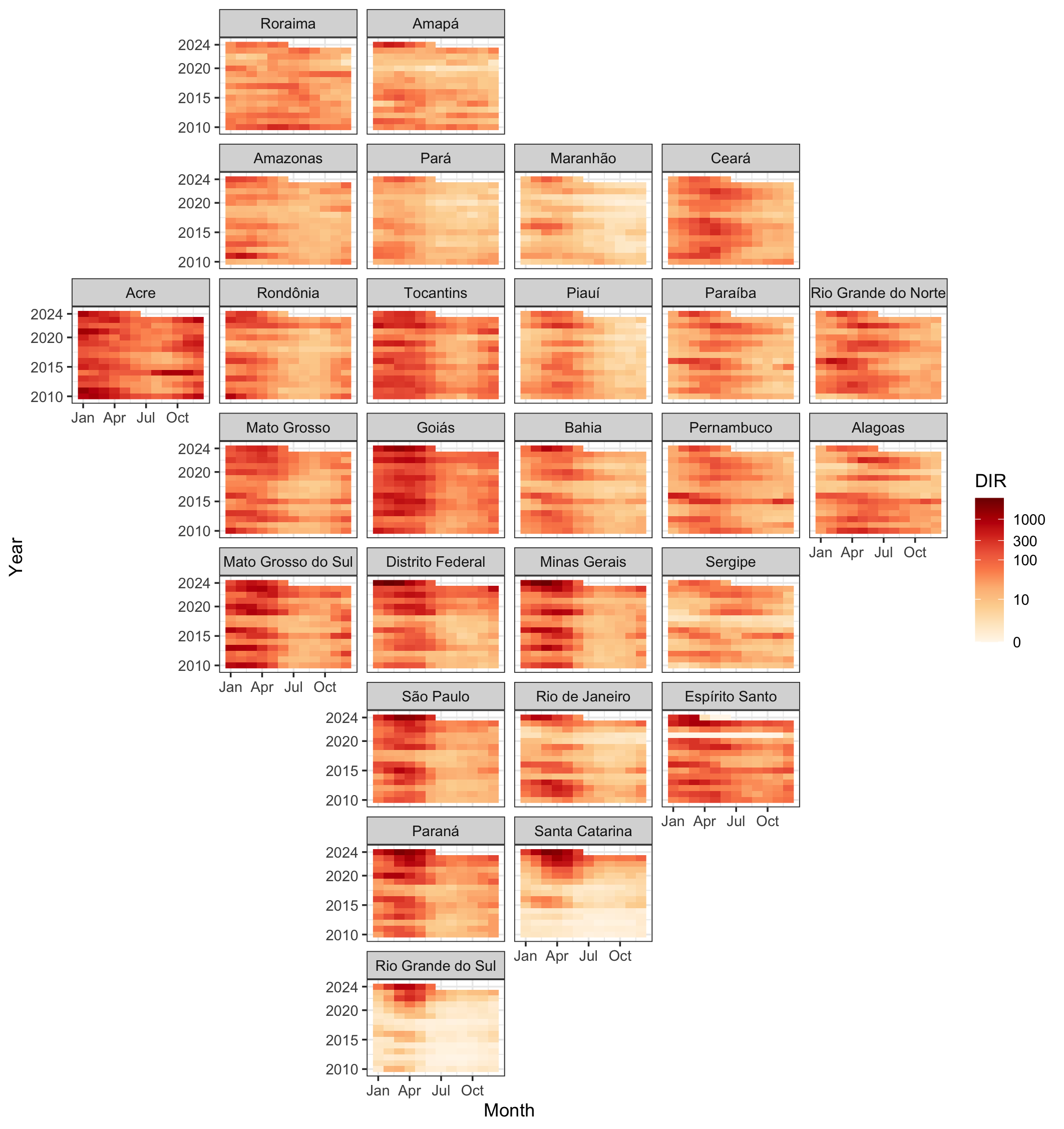
Dengue incidence rate (cases per 100k people) on log10 scale in 27 Brazilian states, Jan 2010 to Jul 2024
Climate covariates
We utilize a suite of covariates known to affect dengue transmission
from the Copernicus ERA5 Reanalysis Data summarized by week
| Variable | Unit | Description |
|---|---|---|
| Minimum Temperature | °C | Lowest temperature recorded within the week, based on reanalysis hourly data. |
| Mean Temperature | °C | Average temperature across the week. |
| Maximum Temperature | °C | Highest temperature recorded within the week. |
| Minimum Precipitation Rate | mm/h | Lowest hourly precipitation rate recorded during the week. |
| Average Precipitation Rate | mm/h | Weekly average of hourly precipitation rates. |
| Maximum Precipitation Rate | mm/h | Highest hourly precipitation rate recorded during the week. |
| Total Precipitation | mm | Cumulative precipitation over the week. |
| Minimum Atmospheric Pressure | atm | Lowest atmospheric pressure measured at sea level during the week. |
| Average Atmospheric Pressure | atm | Weekly mean atmospheric pressure at sea level. |
| Maximum Atmospheric Pressure | atm | Highest atmospheric pressure measured at sea level during the week. |
| Minimum Relative Humidity | % | Lowest relative humidity value recorded during the week. |
| Mean Relative Humidity | % | Weekly average relative humidity. |
| Maximum Relative Humidity | % | Highest relative humidity recorded during the week. |
| Thermal Range | °C | Difference between the daily maximum and minimum temperatures. |
| Rainy Days | Days | Number of days within the week where the total precipitation exceeded 0.03 mm. |
Borrowing information from neighbors
Neighbors assumed to be regions sharing a common boundary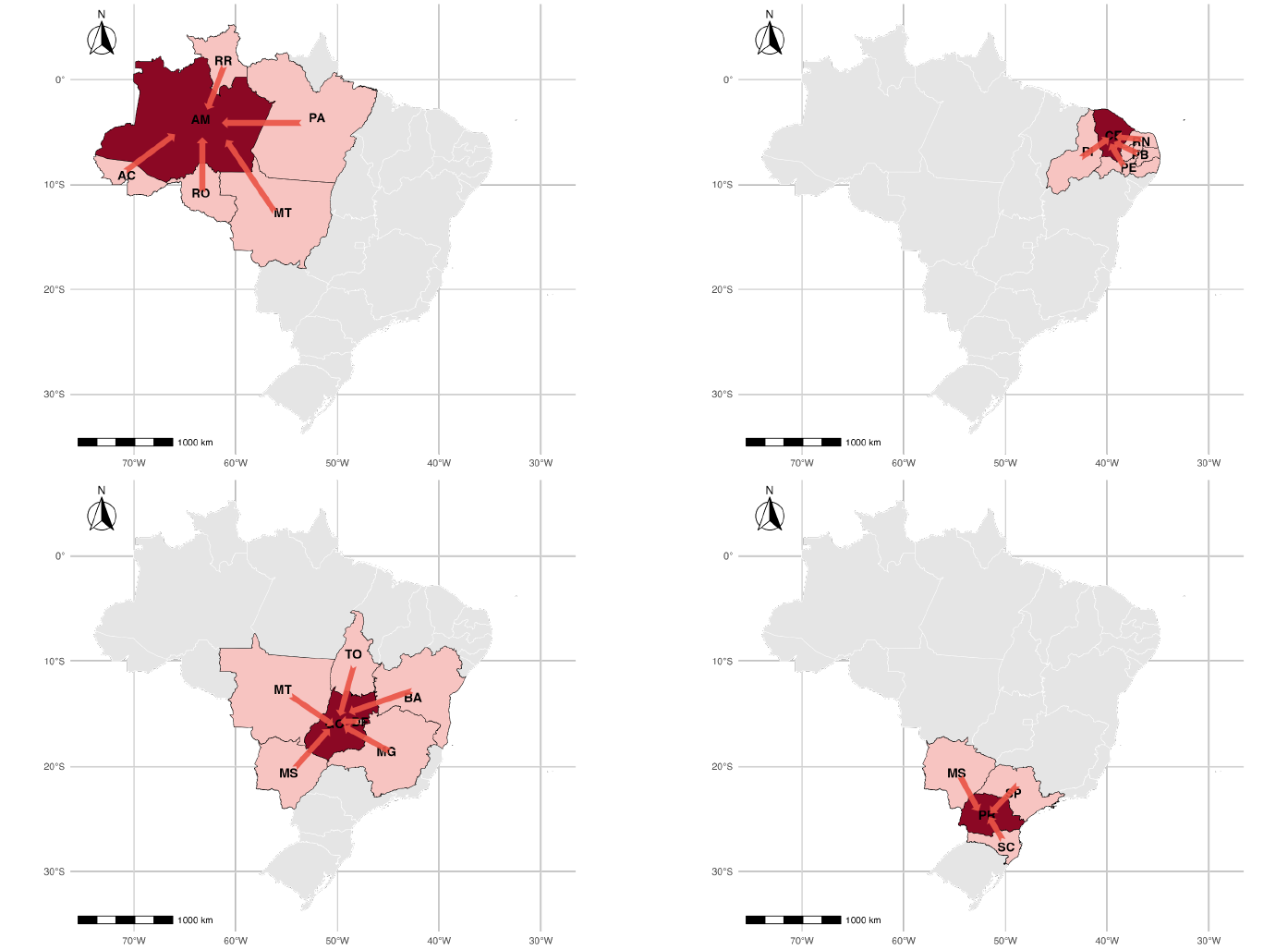
Goias: Tocantins, Bahia, Minas Gerais, Mato Grosso, Mato Grosso do Sul and Distrito Federal
Method’s performance assessment
We use the first 6 years (i.e., 2016-01-03 to 2021-12-26) to predict the number of dengue cases 1, 2, 3, 4, 8 and 12 weeks ahead. Then, we move the window one week keeping 6 years fixed for training to predict the number of cases weeks ahead until 2023-12-24.
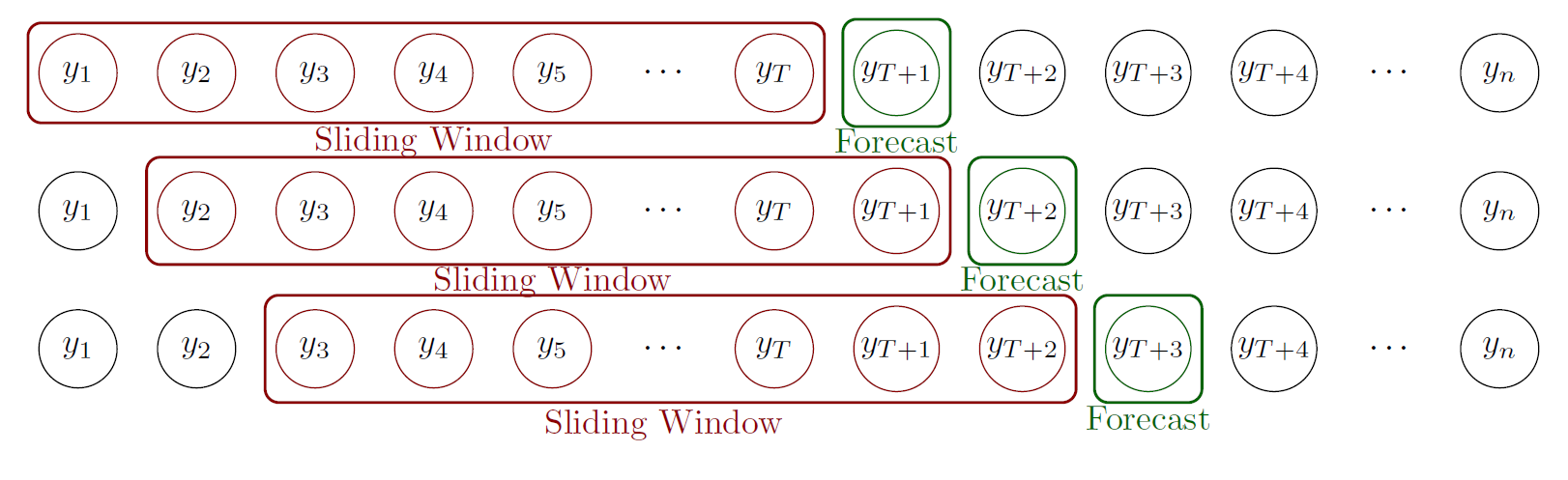
We conduct a performance assessment of the method in comparison with alternative approaches
\(\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|\) \(\text{MAPE} = \frac{100\%}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right|\) \(\text{CRPS}(\mathcal{N}(\mu_i, \sigma^2_i), y_i) = \sigma_i \left ( \omega_i[\Phi(\omega_i) - 1] + 2\phi(\omega_i) - \frac{1}{\sqrt{\pi}}\right )\)
For week \(i\), \(y_i\) observed cases, \(\mu_i\) mean forecast, \(\sigma_i\) standard deviation of forecast (width/2 of the CI).
\(\Phi(\omega_i)\) CDF and \(\phi(\omega_i)\) PDF of standard normal evaluated at the normalized prediction error \(\omega_i = (y_i - \mu_i)/\sigma_i\).
Results
Methods perform well overall except in Amazon regions which are less well connected with their neighbors
Performance measures forecasts 4-weeks ahead
| Federal Unit (FU) | Code | LSTM-Cases | LSTM-Climate | LSTM-Climate-Spatial | Bayesian Baseline | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MAPE | CRPS | MAE | MAPE | CRPS | MAE | MAPE | CRPS | MAE | MAPE | CRPS | ||
| Acre (AC) | 12 | 305.19 | 45.50% | 90.91 | 129.76 | 22.30% | 35.68 | 136.83 | 24.89% | 37.34 | 382.77 | 47.23% | 96.13 |
| Alagoas (AL) | 27 | 177.96 | 43.29% | 38.14 | 79.24 | 30.54% | 16.27 | 61.08 | 23.17% | 12.98 | 69.39 | 24.28% | 13.41 |
| Amapá (AP) | 16 | 51.21 | 47.90% | 34.05 | 22.45 | 23.49% | 5.35 | 27.45 | 26.98% | 6.02 | 30.53 | 34.09% | 7.12 |
| Amazonas (AM) | 13 | 188.17 | 41.56% | 32.14 | 100.21 | 19.63% | 19.23 | 111.60 | 21.64% | 22.44 | 143.57 | 28.79% | 31.40 |
| Bahia (BA) | 29 | 886.64 | 29.94% | 165.30 | 639.44 | 23.20% | 123.86 | 532.46 | 17.13% | 120.50 | 718.63 | 22.84% | 137.74 |
| Ceará (CE) | 23 | 562.67 | 46.52% | 108.09 | 245.17 | 27.54% | 52.99 | 187.56 | 15.51% | 35.01 | 315.69 | 30.16% | 60.26 |
| Distrito Federal (DF) | 53 | 1040.21 | 26.69% | 244.60 | 926.73 | 23.24% | 219.97 | 767.30 | 16.72% | 211.70 | 997.42 | 24.57% | 249.25 |
| Espírito Santo (ES) | 32 | 8431.94 | 30.90% | 1713.56 | 7262.14 | 30.35% | 1310.95 | 6300.78 | 23.06% | 1308.43 | 6967.74 | 25.93% | 1552.96 |
| Goiás (GO) | 52 | 1708.00 | 30.34% | 310.44 | 1277.24 | 27.36% | 226.00 | 1195.70 | 19.87% | 222.87 | 1722.08 | 29.75% | 321.36 |
| Maranhão (MA) | 21 | 143.59 | 56.31% | 26.44 | 102.87 | 38.07% | 18.93 | 59.27 | 23.91% | 10.88 | 147.31 | 53.05% | 28.14 |
| Mato Grosso (MT) | 51 | 657.81 | 34.65% | 189.42 | 563.40 | 26.97% | 142.56 | 340.72 | 16.69% | 72.73 | 624.21 | 28.36% | 125.27 |
| Mato Grosso do Sul (MS) | 50 | 1711.05 | 75.23% | 342.47 | 568.10 | 59.97% | 108.71 | 404.48 | 40.11% | 81.94 | 1646.17 | 50.03% | 344.61 |
| Minas Gerais (MG) | 31 | 15099.46 | 52.28% | 3253.80 | 7730.47 | 33.33% | 1648.53 | 5088.71 | 24.52% | 1035.86 | 14220.67 | 40.19% | 3472.85 |
| Pará (PA) | 15 | 319.85 | 47.03% | 72.72 | 256.88 | 26.23% | 53.97 | 159.61 | 19.43% | 34.75 | 210.77 | 21.89% | 56.14 |
| Paraná (PR) | 41 | 651.62 | 44.56% | 145.98 | 532.44 | 26.62% | 104.80 | 391.02 | 20.01% | 81.55 | 603.78 | 22.63% | 117.92 |
| Pernambuco (PE) | 26 | 501.76 | 41.95% | 96.53 | 358.33 | 32.90% | 69.27 | 257.65 | 19.53% | 58.65 | 355.72 | 26.02% | 72.60 |
| Piauí (PI) | 22 | 319.75 | 43.87% | 57.96 | 263.10 | 30.81% | 50.76 | 194.54 | 20.75% | 41.58 | 298.91 | 28.17% | 57.16 |
| Rio de Janeiro (RJ) | 33 | 1034.84 | 32.60% | 217.36 | 861.35 | 25.10% | 194.52 | 717.22 | 18.02% | 175.08 | 910.87 | 22.58% | 210.46 |
| Rio Grande do Norte (RN) | 24 | 313.87 | 49.58% | 68.70 | 252.68 | 30.67% | 47.31 | 171.49 | 19.76% | 35.35 | 259.23 | 24.48% | 49.58 |
| Rio Grande do Sul (RS) | 43 | 823.57 | 31.88% | 155.09 | 679.61 | 28.42% | 122.36 | 548.03 | 21.42% | 98.53 | 736.82 | 25.74% | 149.61 |
| Rondônia (RO) | 11 | 371.50 | 79.49% | 103.44 | 300.93 | 42.08% | 79.71 | 285.61 | 40.93% | 69.17 | 323.33 | 43.03% | 104.34 |
| Roraima (RR) | 14 | 9.33 | 40.63% | 6.03 | 6.52 | 43.27% | 5.02 | 6.36 | 44.31% | 5.93 | 8.66 | 52.55% | 2.55 |
| Santa Catarina (SC) | 42 | 7381.10 | 79.16% | 1765.31 | 1585.71 | 56.28% | 395.28 | 1556.58 | 15.21% | 294.09 | 3028.00 | 40.68% | 831.25 |
| São Paulo (SP) | 35 | 9544.39 | 49.61% | 2196.34 | 4088.67 | 31.97% | 921.95 | 3068.46 | 17.28% | 612.34 | 8468.53 | 31.64% | 1961.50 |
| Sergipe (SE) | 28 | 54.35 | 20.82% | 13.07 | 45.92 | 17.48% | 9.43 | 41.52 | 16.50% | 8.11 | 86.08 | 31.38% | 18.57 |
| Tocantins (TO) | 17 | 124.25 | 49.07% | 31.51 | 103.21 | 37.89% | 28.46 | 92.55 | 29.12% | 20.44 | 128.97 | 45.07% | 27.20 |
Mobility
Comprehensive dataset on intercity mobility spanning air, road, and waterway transport (Oliveira et al. The Lancet Digital Health, 2024)
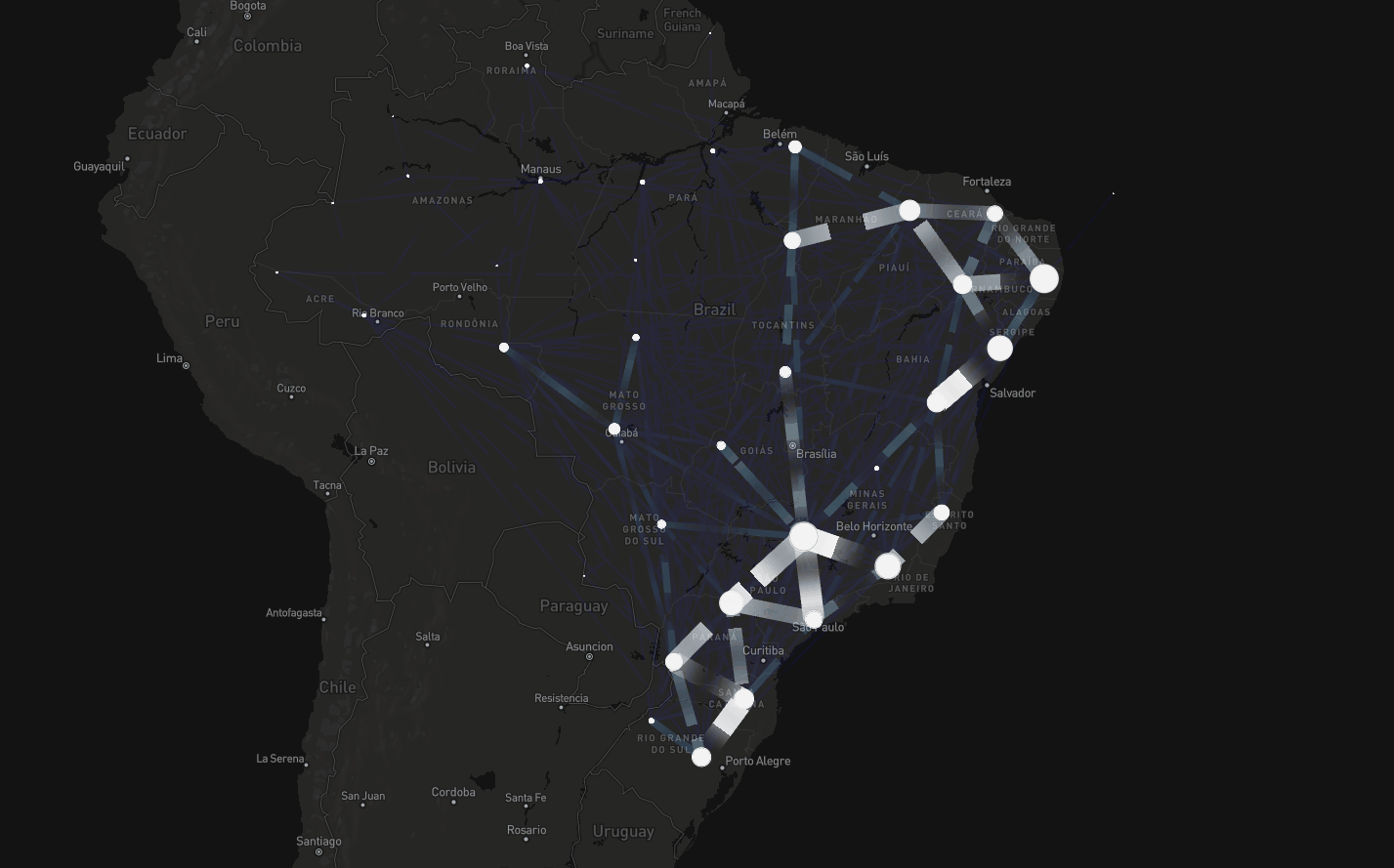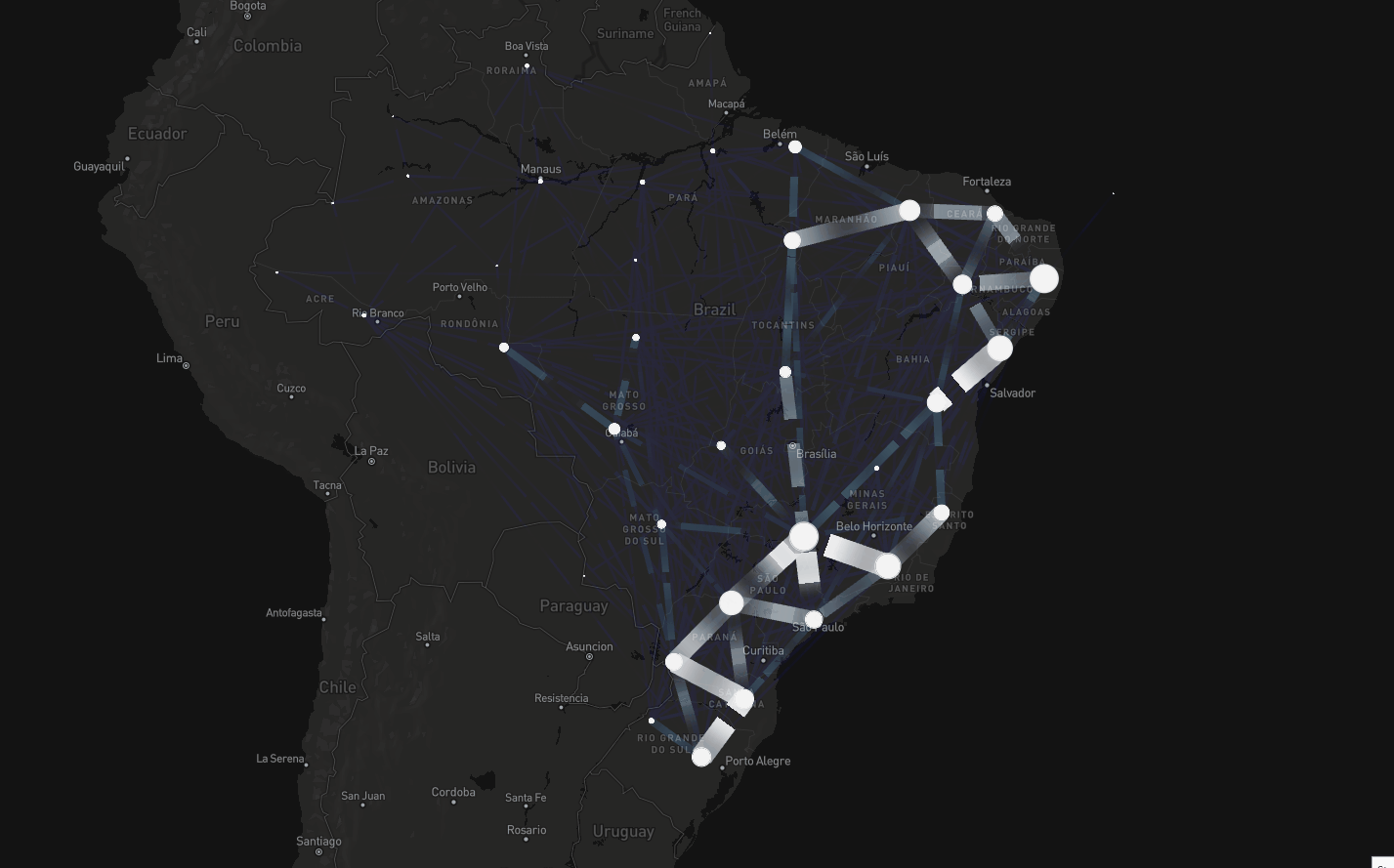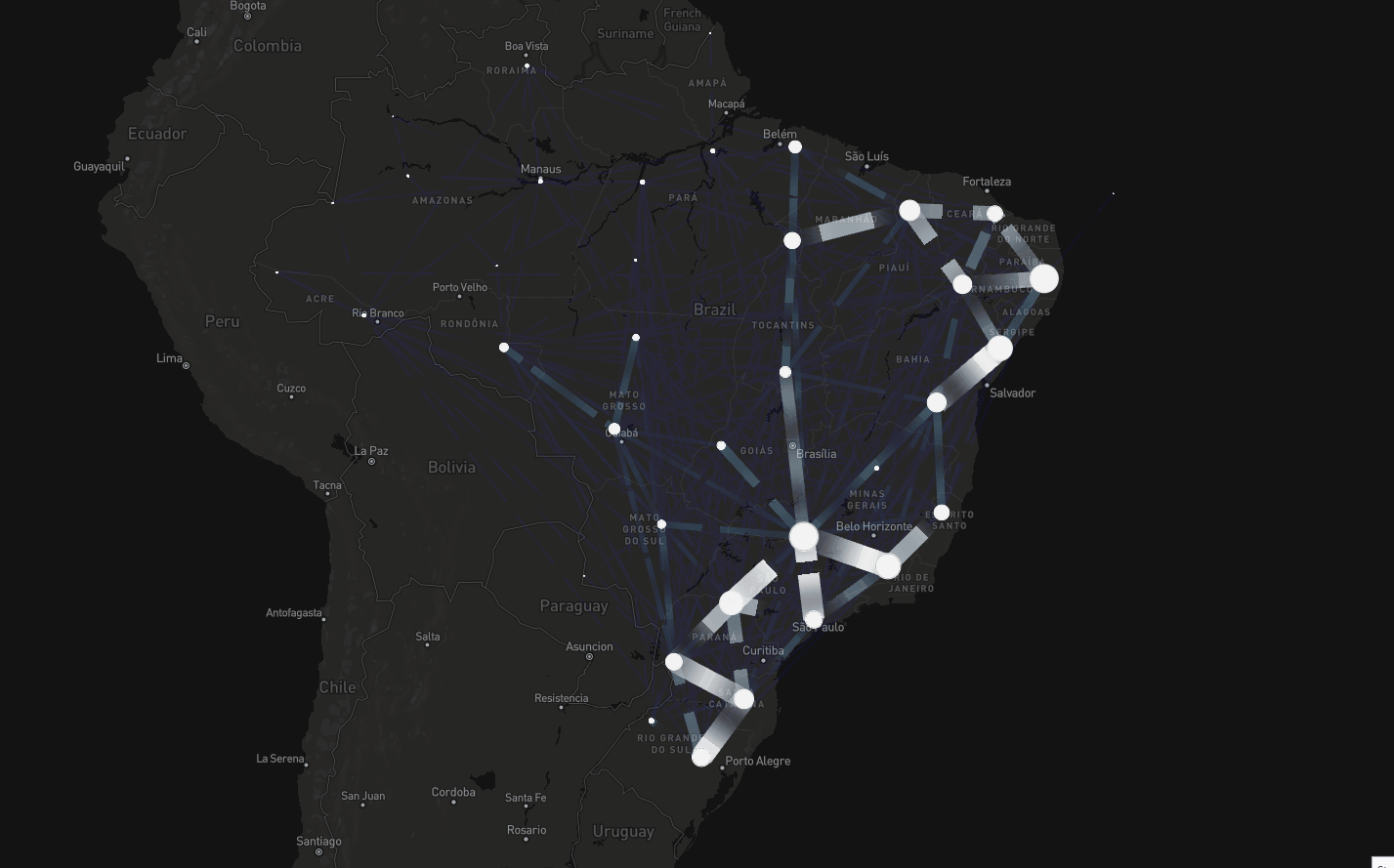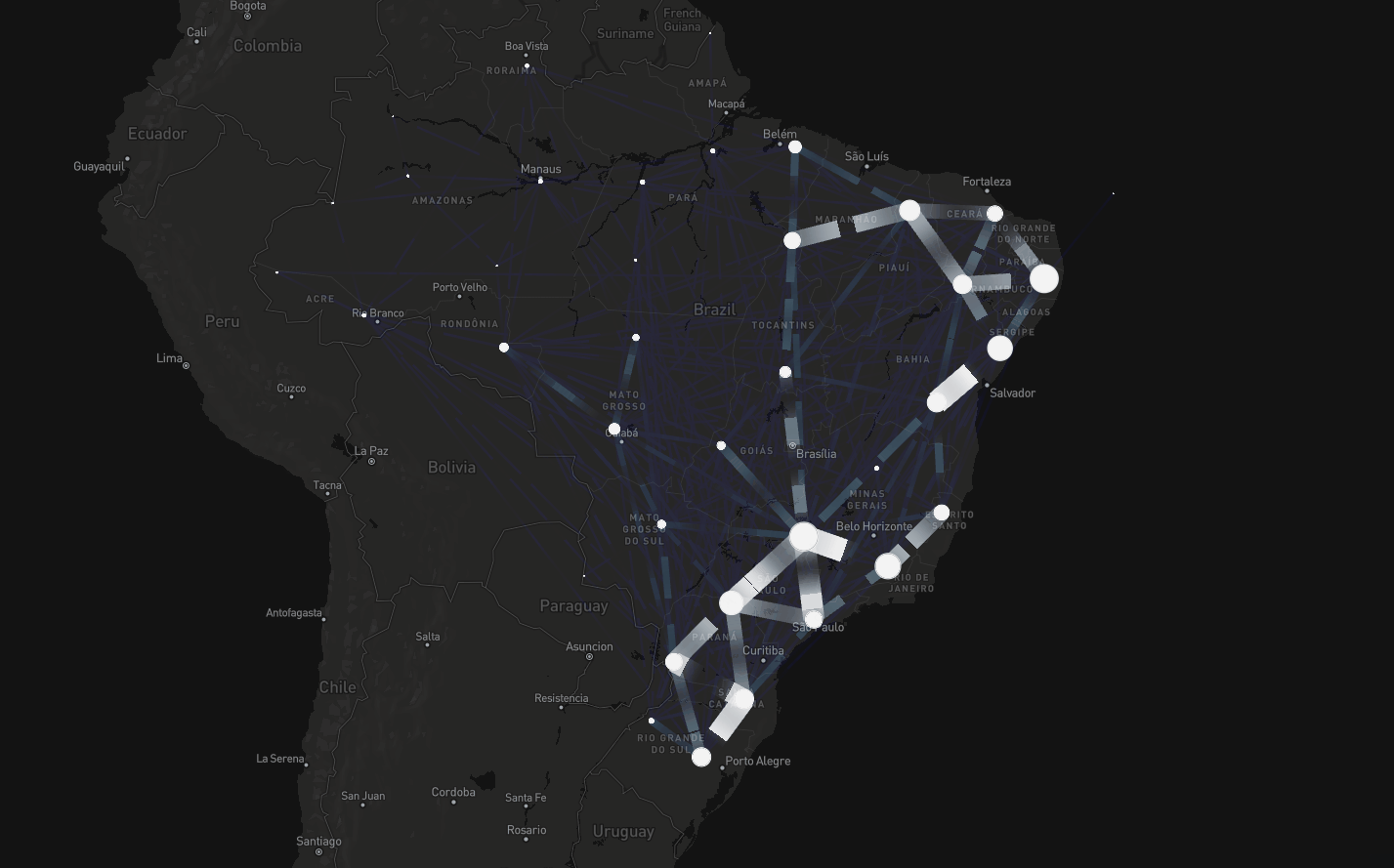
Deep Learning and mobility data
Consider contribution of cases imported into each city \(i\) from others in week \(t\): \[ \text{Imported Cases}_{i, t} = \sum_{j \in \mathcal{N}_i} \text{Mobility}_{ji} \cdot \frac{\text{Cases}_{j, t}}{\text{Population}_j} \]
\(\mathcal{N}_i\): set of cities with connections with city \(i\), \(\text{Mobility}_{ji}\): people from city \(j\) to \(i\), \(\text{Cases}_{j, t}\): number cases in city \(j\) and week \(t\), \(\text{Population}_j\) city \(j\)
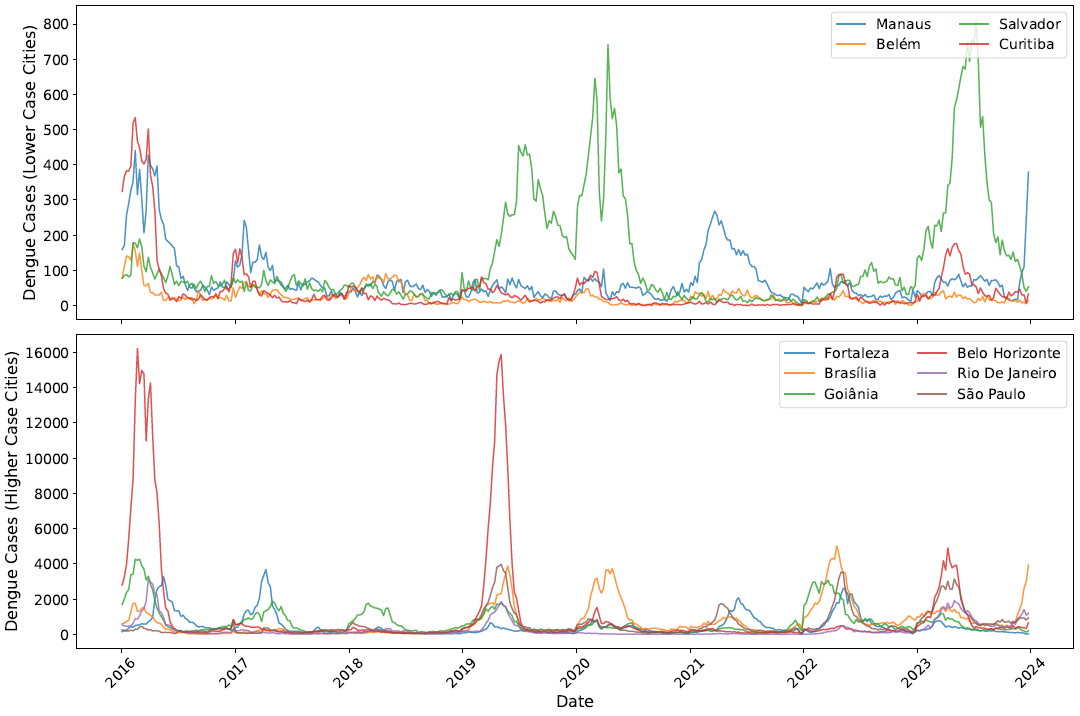
Selected cities
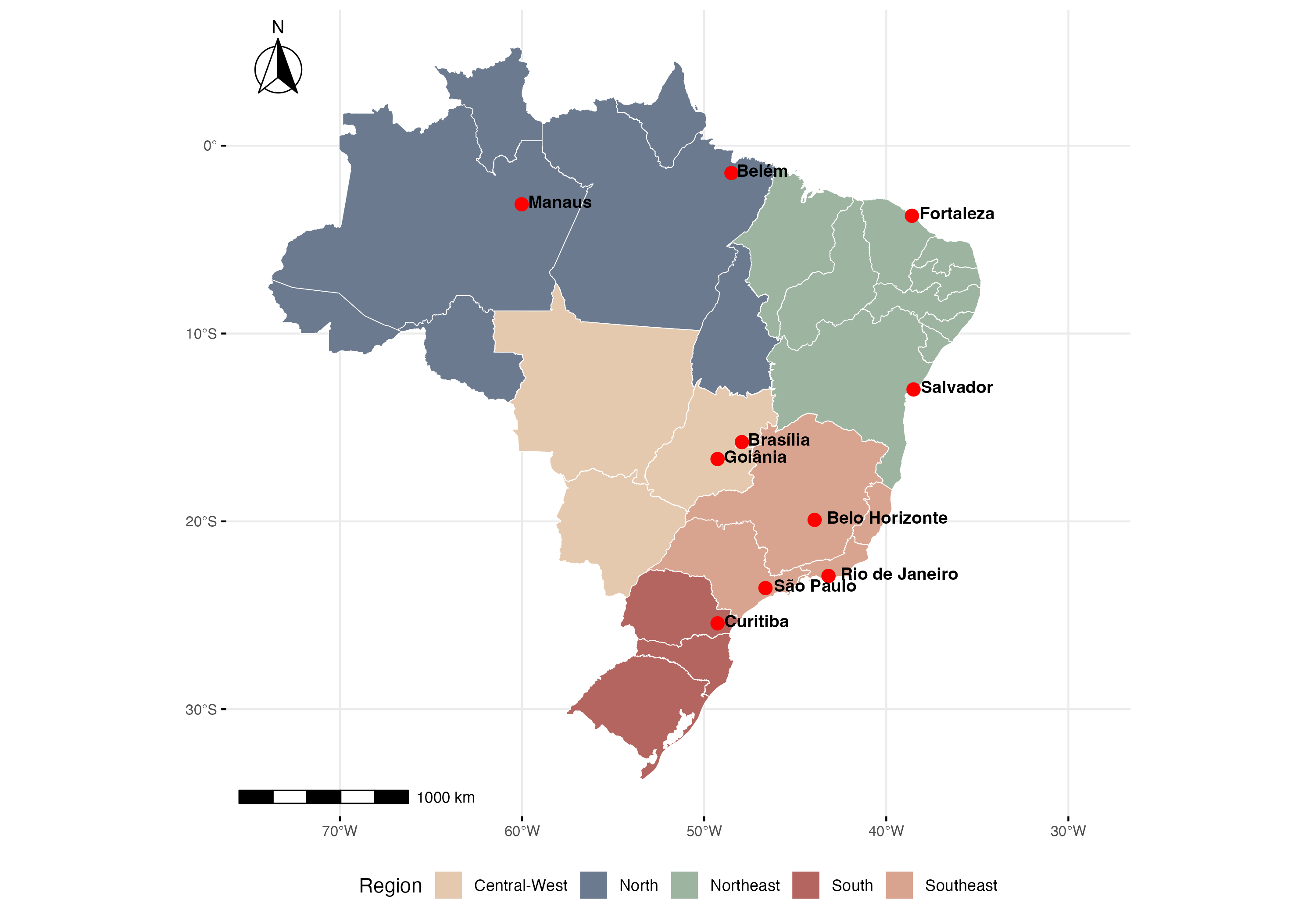
|
|
- Northern (Manaus, Belém): equatorial climate, high humidity, and persistent rainfall, favorable environment for mosquitoes
- Northeastern (Fortaleza, Salvador): tropical and semi-arid climates, with seasonal dengue outbreaks driven by fluctuations in rainfall and temperature
- Central-West (Brasília, Goiânia): tropical savanna climate, with a distinct dry season and strong temperature variations, influencing mosquito breeding and disease transmission
- Southeastern (Belo Horizonte, Rio de Janeiro, São Paulo): highly urbanized with humid subtropical and tropical climates, making it a significant contributor to national dengue cases
- Southern (Curitiba): traditionally less affected by dengue, but recent epidemiological shifts indicate an increasing number of cases, likely driven by climate change and urbanization
Forecasting results model including mobility
| City | State |
Baseline 1 (cases) |
Baseline 2 (cases + climate) |
Baseline 3 (cases + climate + neighbors) |
Model (cases + climate + mobility) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | MAPE | CRPS | MAE | MAPE | CRPS | MAE | MAPE | CRPS | MAE | MAPE | CRPS | ||
| Manaus | AM | 98.16 | 42.89% | 22.74 | 80.38 | 31.32% | 16.72 | 78.31 | 30.00% | 16.58 | 75.45 | 29.95% | 15.31 |
| Belém | PA | 28.11 | 40.09% | 6.00 | 24.77 | 32.30% | 5.20 | 25.64 | 30.03% | 5.19 | 23.98 | 29.28% | 5.19 |
| Fortaleza | CE | 428.81 | 38.01% | 93.73 | 361.72 | 29.66% | 79.32 | 277.54 | 26.20% | 71.61 | 247.27 | 22.59% | 68.95 |
| Salvador | BA | 386.72 | 39.24% | 79.06 | 299.63 | 30.95% | 56.97 | 252.09 | 25.14% | 52.54 | 228.55 | 23.95% | 47.91 |
| Brasília | DF | 1480.98 | 35.05% | 327.45 | 1359.57 | 31.11% | 308.13 | 1276.06 | 27.24% | 281.61 | 1067.66 | 22.12% | 213.89 |
| Goiânia | GO | 604.09 | 35.64% | 129.50 | 547.72 | 29.22% | 107.42 | 524.47 | 25.47% | 93.17 | 439.02 | 23.26% | 88.87 |
| Belo Horizonte | MG | 2360.34 | 39.28% | 480.91 | 1555.45 | 34.74% | 283.63 | 1501.73 | 28.24% | 267.42 | 1483.27 | 22.47% | 257.55 |
| Rio de Janeiro | RJ | 1153.40 | 39.78% | 189.70 | 1210.43 | 31.60% | 170.82 | 1010.78 | 27.82% | 168.70 | 819.73 | 21.87% | 158.93 |
| São Paulo | SP | 1812.24 | 35.65% | 348.72 | 1490.23 | 30.61% | 275.45 | 1230.09 | 24.84% | 227.07 | 1102.75 | 22.18% | 205.74 |
| Curitiba | PR | 101.61 | 38.55% | 20.20 | 77.79 | 34.55% | 14.81 | 70.21 | 27.22% | 14.21 | 65.99 | 25.33% | 13.11 |
Conclusions
- Developed a forecasting model that improves accuracy by integrating historical cases, climate and human mobility. Model is generalizable and can be applied to other regions and diseases influenced by climate and mobility. Supports data-driven early warning systems for public health surveillance
- Findings in open access papers, and code freely available for reproducibility



Translation of research into action and inform policymaking
Forecasting 2025 dengue cases in Brazil
We participated in the Infodengue-Mosqlimate Dengue Challenge (IMDC) to produce actionable forecasts of the 2025 dengue season to help inform the Brazilian Ministry of Health its response and surveillance activities
These predictions helped the Brazilian Ministry of Health have more time to be prepared and allocate resources in areas of greatest need and to reduce disease impacts
Ensemble forecast for dengue in Brazil, 2025


We collaborated with 6 teams around the world. Each team provided forecasts using a number of statistical and machine learning approaches that leveraged historical data as well as information on climate and environment. Then, individual forecasts were combined to produce a final dengue forecast ensemble for 2025. GitHub Dengue-Forecast-Ensemble
Ensemble forecast for dengue in Brazil, 2025
Predictions for the states of Amazonas (AM), Ceará (CE), Goiás (GO), Paraná (PR), and Minas Gerais (MG)
Dengue forecasting challenge results
The results of the challenge published in September 2024 as a technical report in Portuguese ensuring it reached key decision-makers in Ministry of Health
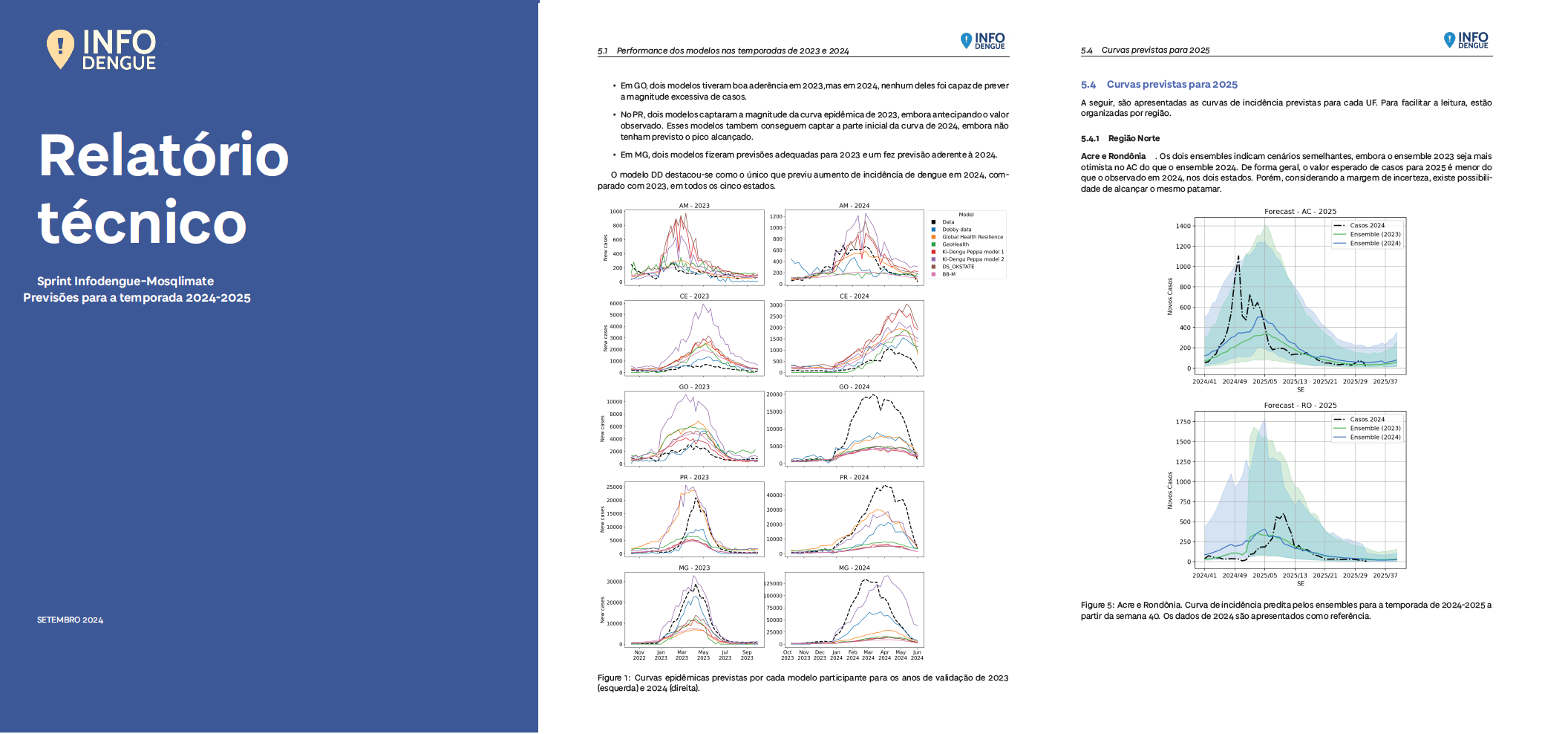
Dengue forecasting challenge results
- Forecasting methods code and results publicly available on GitHub
- Webinars organized to discuss the challenge and its results that were attended by a large number of public health professionals from Brazil
- We continue our collaboration working on better models to provide improved projections for the 2026 dengue season that help inform prevention and control strategies by the Brazilian Ministry of Health

Current work
Precision disease mapping
Disease mapping
Disease mapping is important to understand geographic and temporal patterns of diseases and allocate resources where most needed
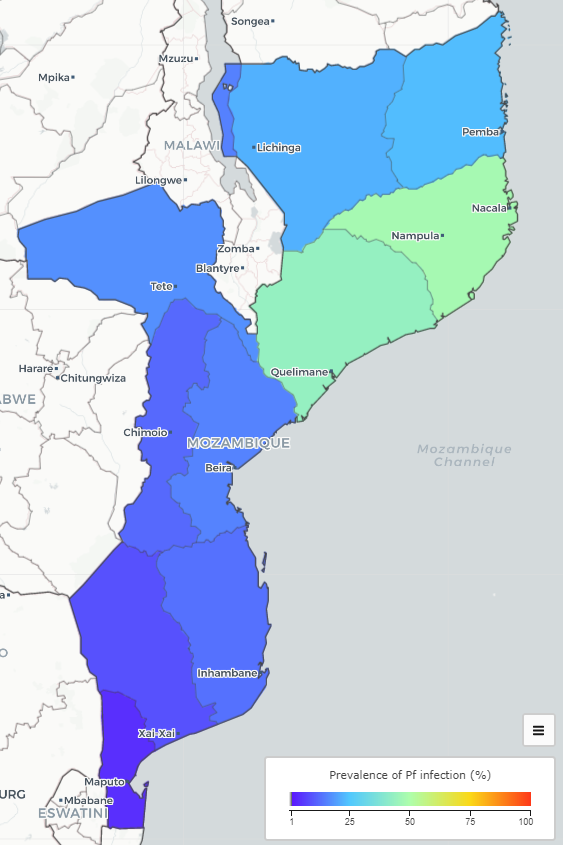
Often, maps given at an areal resolution which difficulties decision-making
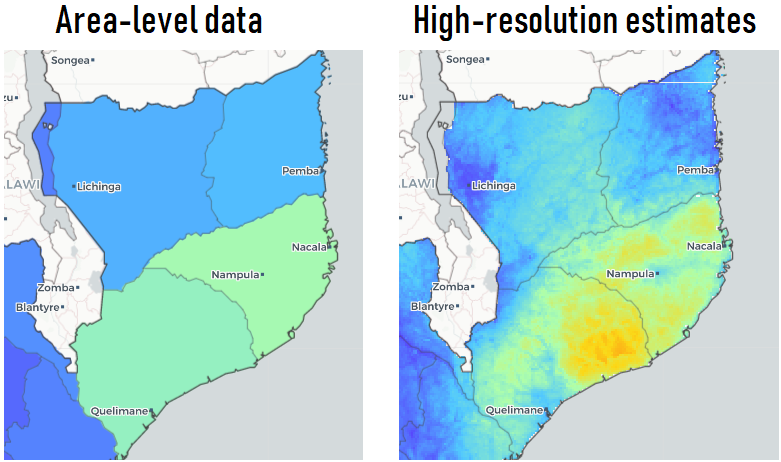
Map shows malaria prevalence in Mozambique. However, disease risk varies continuously in space & areal data unable to show how risk varies within areas
Areal estimates make difficult targeting health interventions and directing resources where most needed
Disaggregate area-level data
High-resolution estimates permit to find differences in disease risk within study regions, and identify areas and groups of people at higher risk
Bayesian spatial disaggregation model
Model assumes there is a spatially continuous variable underlying all observations that can be modeled using a zero-mean Gaussian random field
\[\begin{equation*} \begin{aligned} Y(\mathbf{x}) & \sim \pi \left( \theta(\mathbf{x}), \tau \right), \quad \mathbf{x} \in A \subset \mathbb{R}^2, \\ \theta(\mathbf{x}_i) & = g^{-1}\left(\mu(\mathbf{x}_i)+S\left(\mathbf{x}_i\right) \right), \quad i=1, \ldots, n, \\ \theta(B_i) & =\left|B_i\right|^{-1} \int_{B_i} g^{-1}(\mu (\mathbf{x}) + S(\mathbf{x})) d \mathbf{x}, \quad i=n+1, \ldots, n+m. \end{aligned} \end{equation*}\]
Inference using INLA and a modification of the SPDE approach
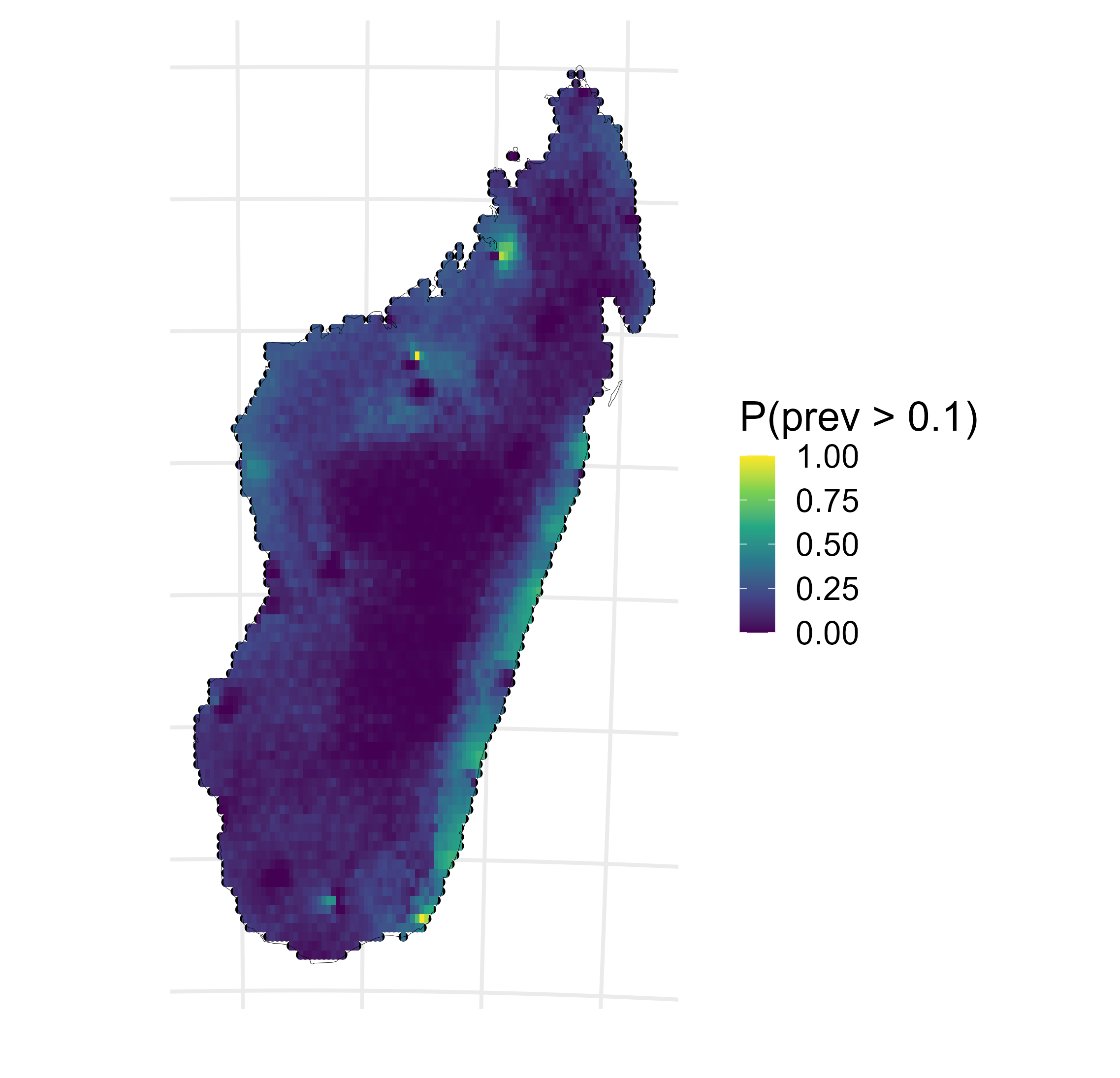
Malaria prevalence in Madagascar
\[\begin{aligned} Y(\mathbf{x}) & \sim \operatorname{Binomial}\left(N(\mathbf{x}), P(\mathbf{x})\right), \quad \mathbf{x} \in A \subset \mathbb{R}^2, \\ P(\mathbf{x_i}) & = \text{logit}^{-1}\left(\mu(\mathbf{x}_i)+S(\mathbf{x}_i)\right), \quad i=1, \ldots, n, \\ P(B_i) & = \left|B_i\right|^{-1} \int_{B_i} \text{logit}^{-1} \left(\mu (\mathbf{x}) + S(\mathbf{x}) \right) d \mathbf{x}, \quad i=n+1, \ldots, n+m. \end{aligned}\]
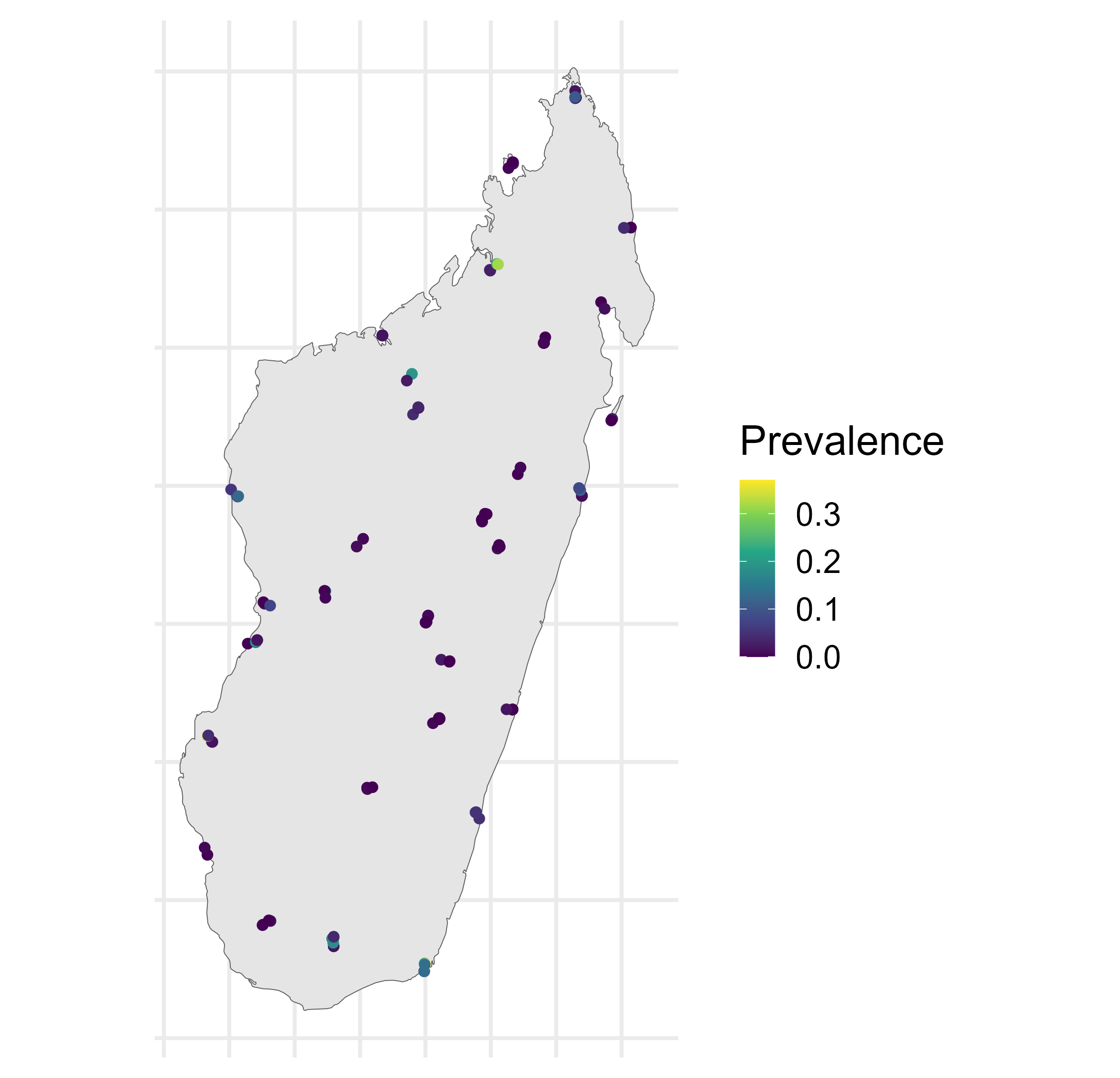
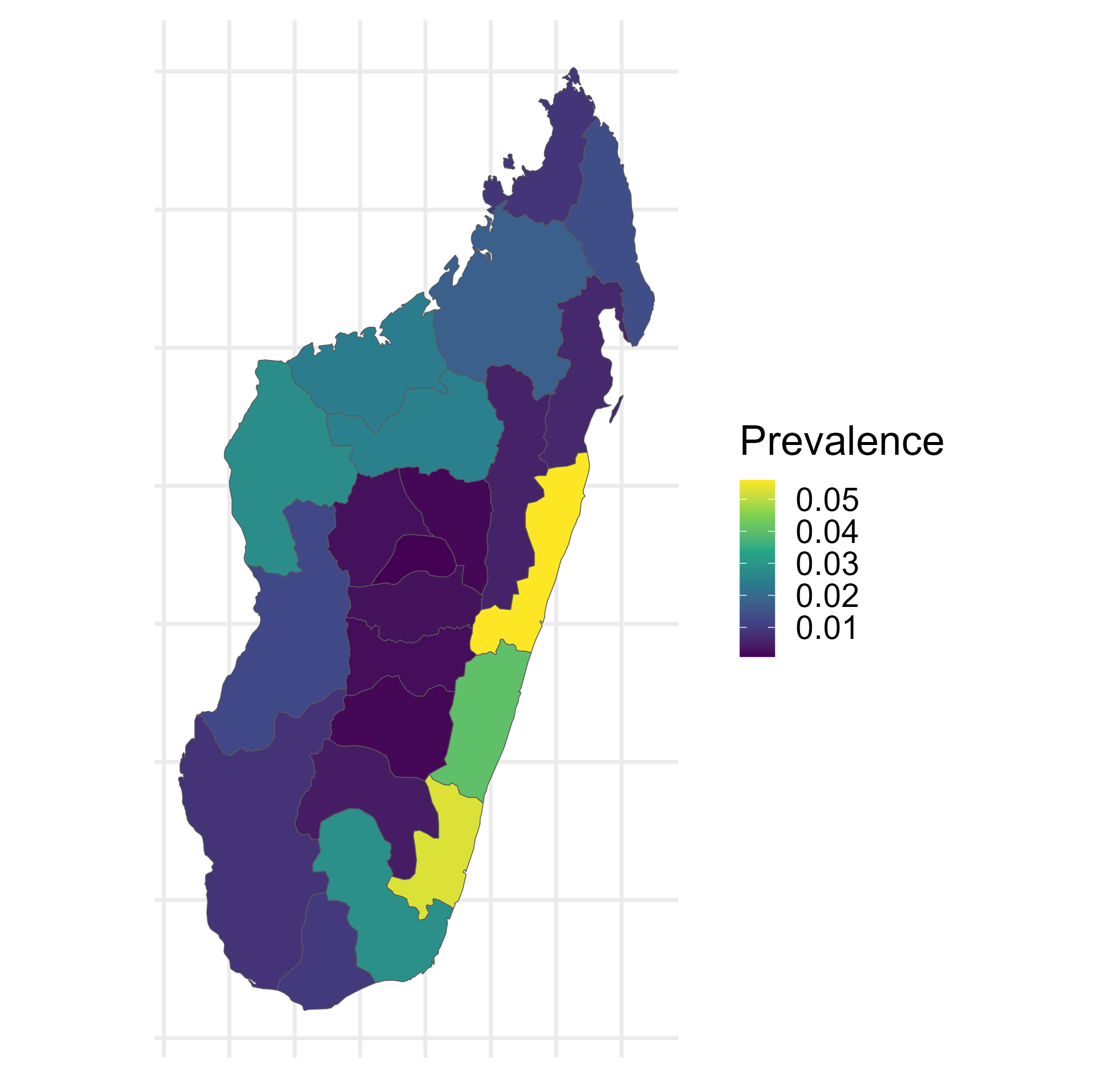
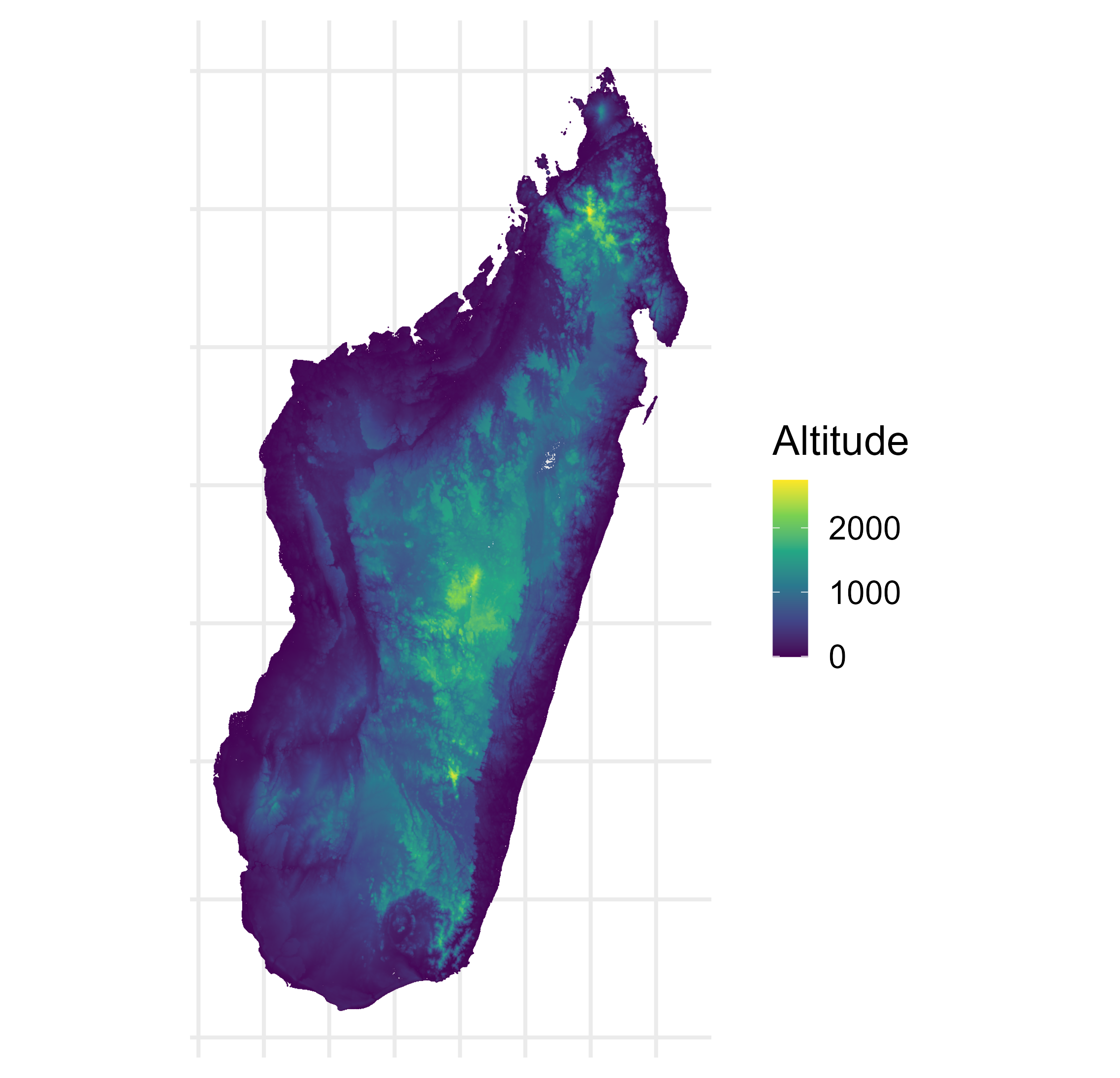
Open-Source Disease Surveillance System
Disease Surveillance System
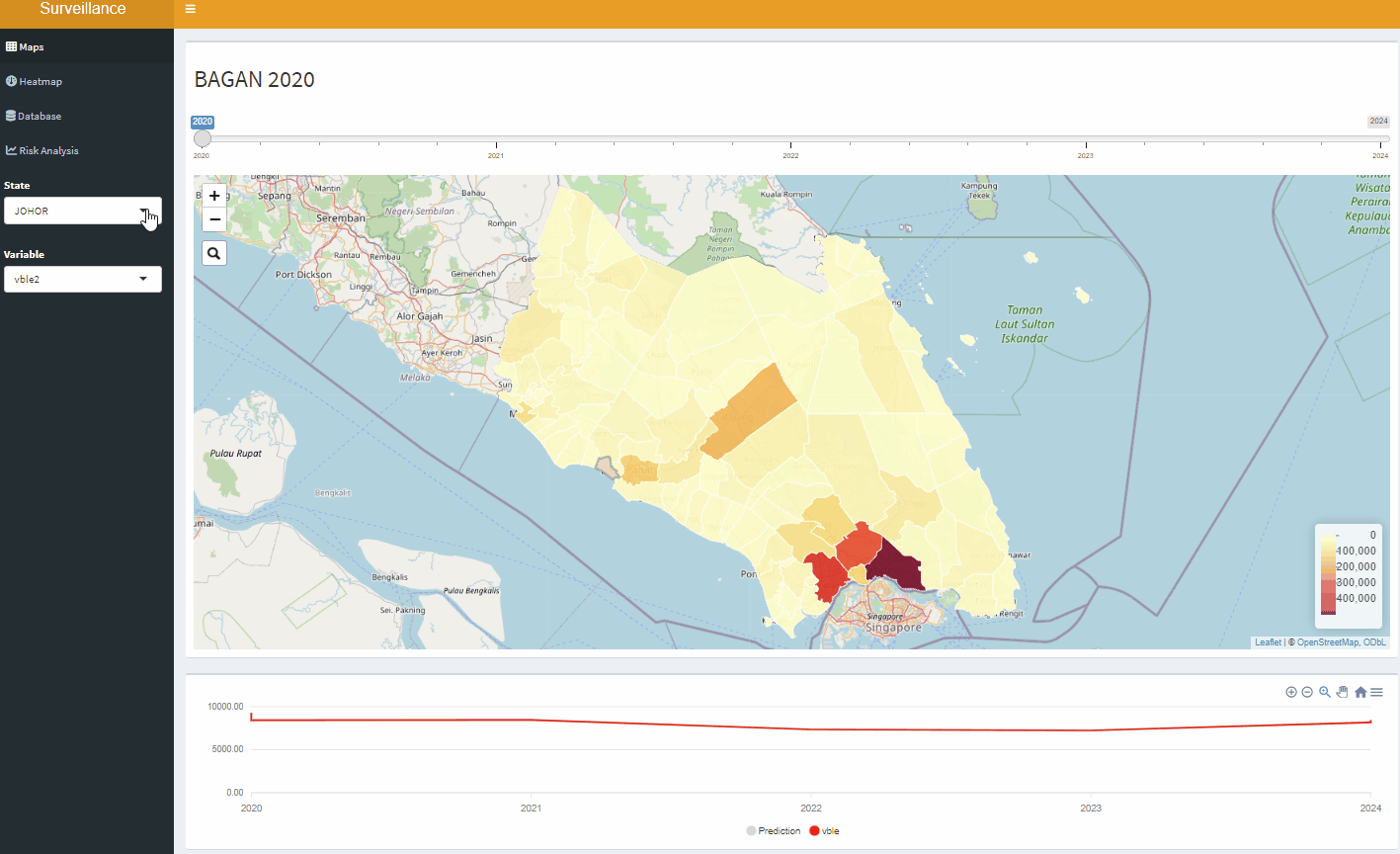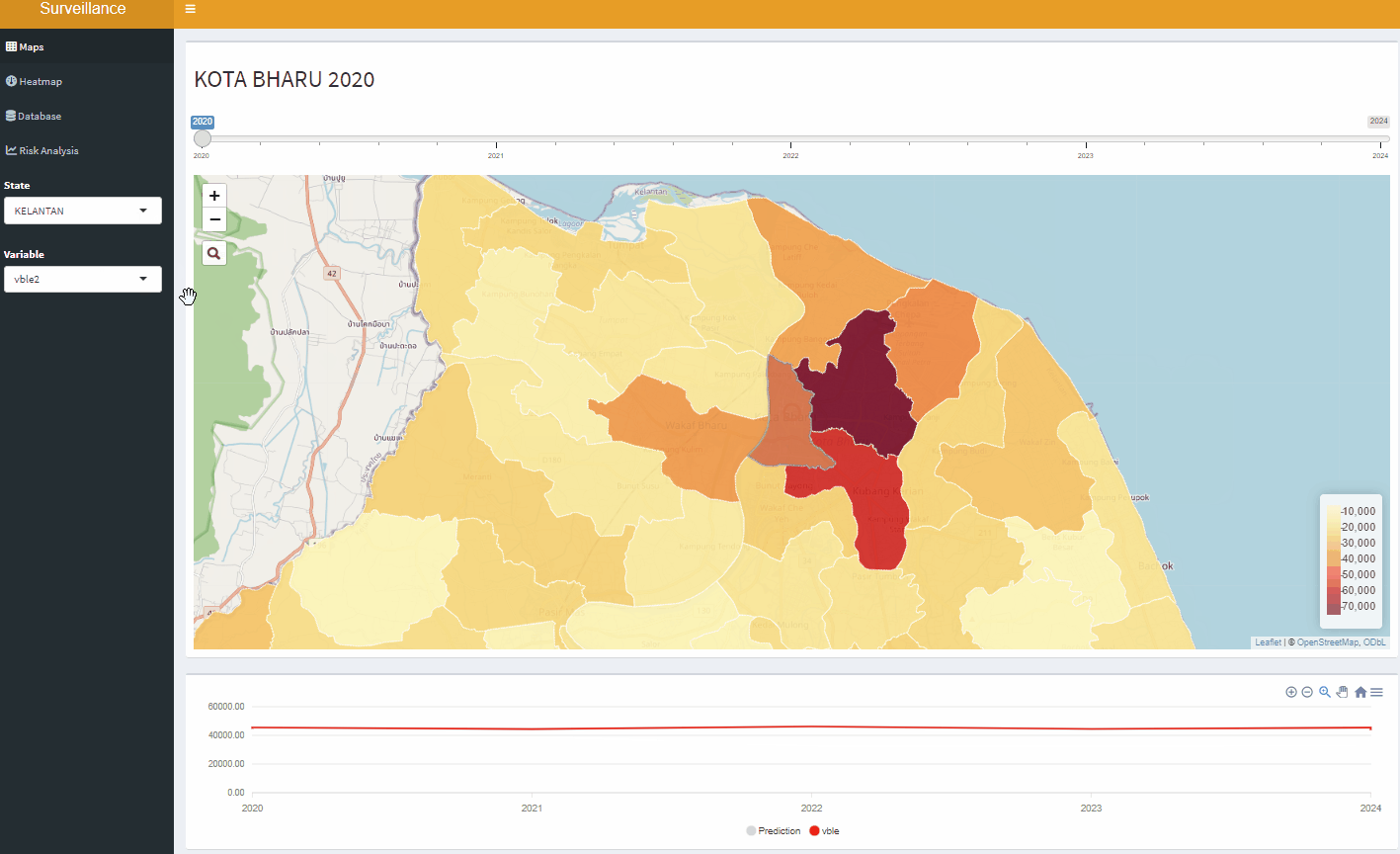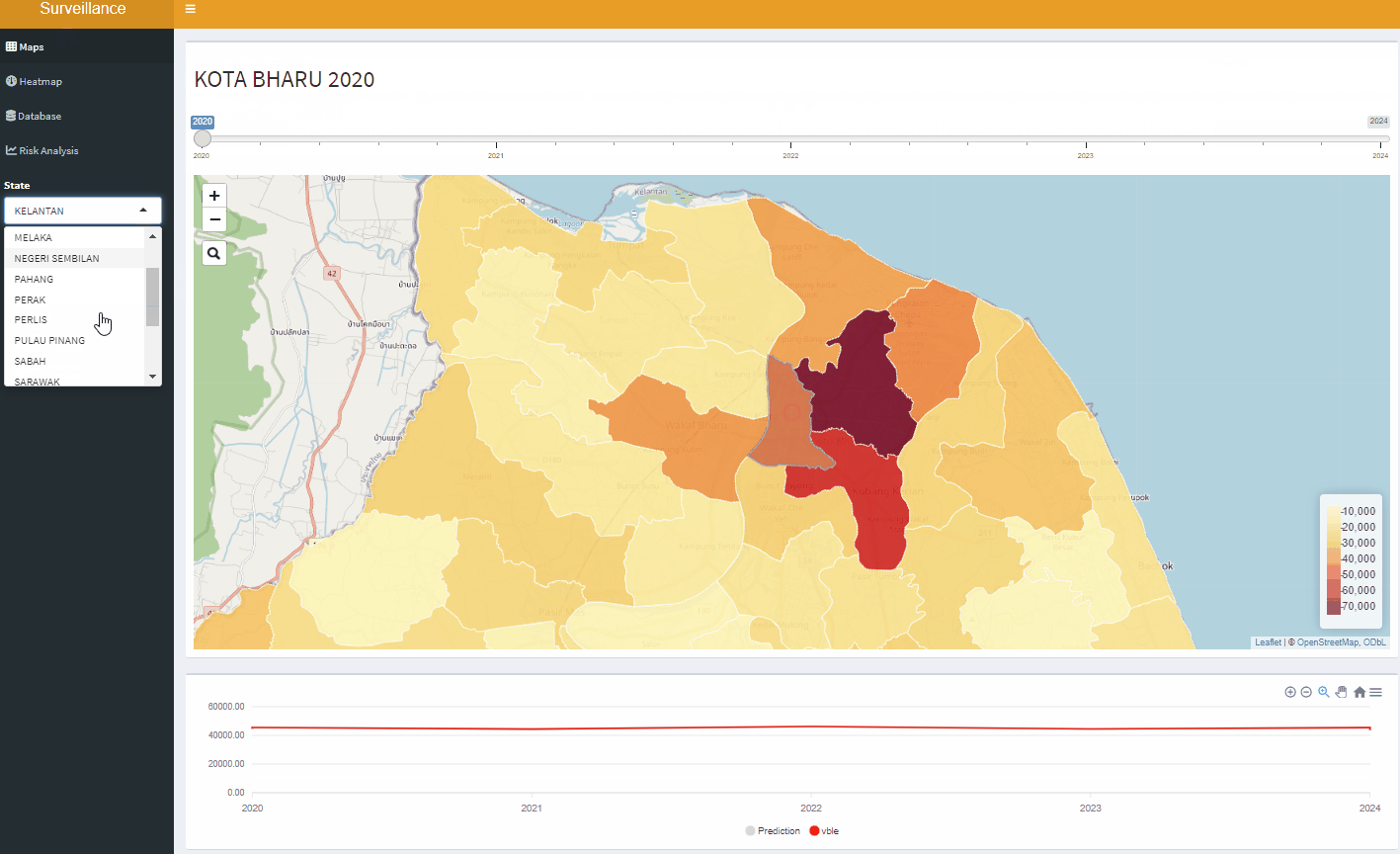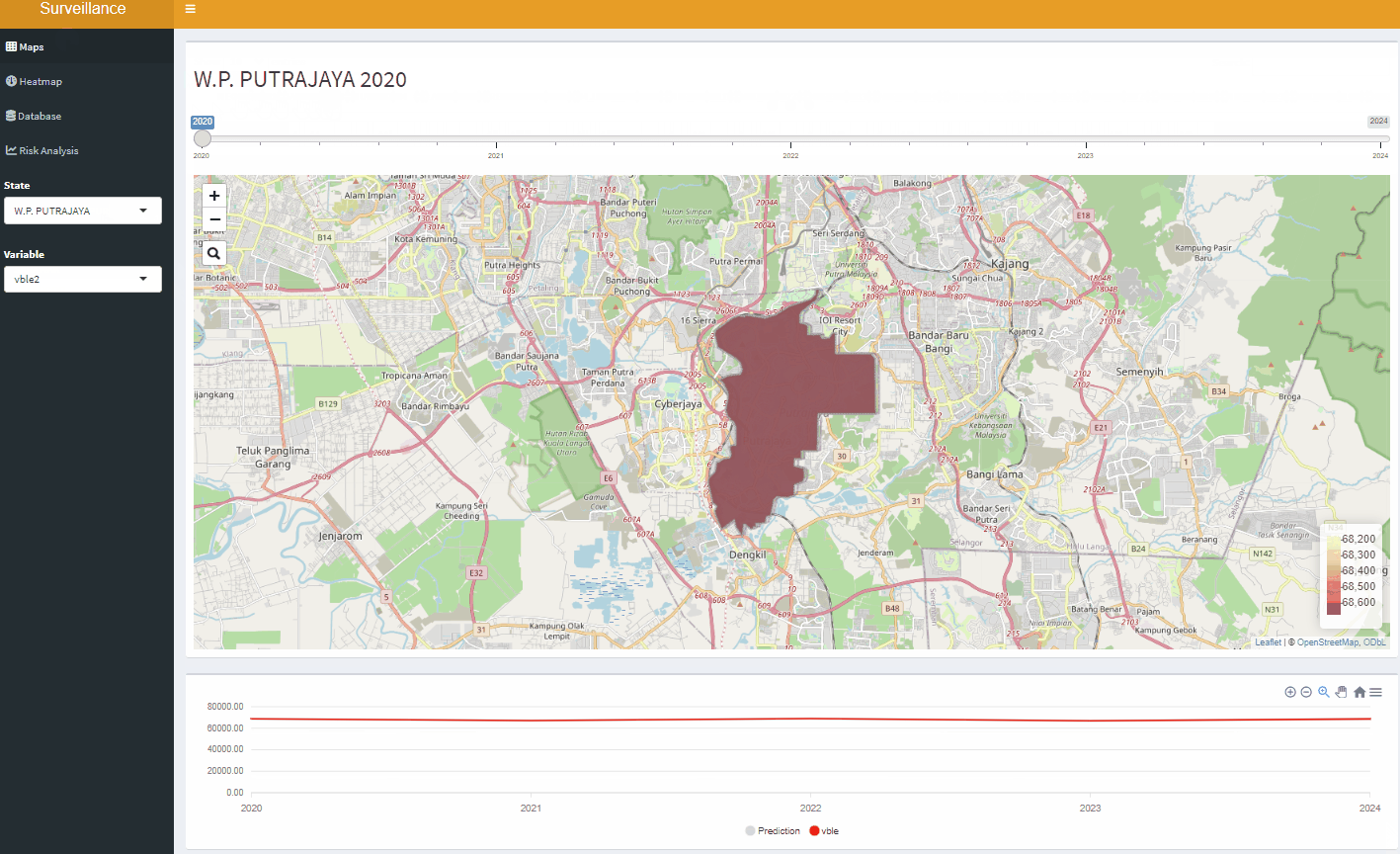
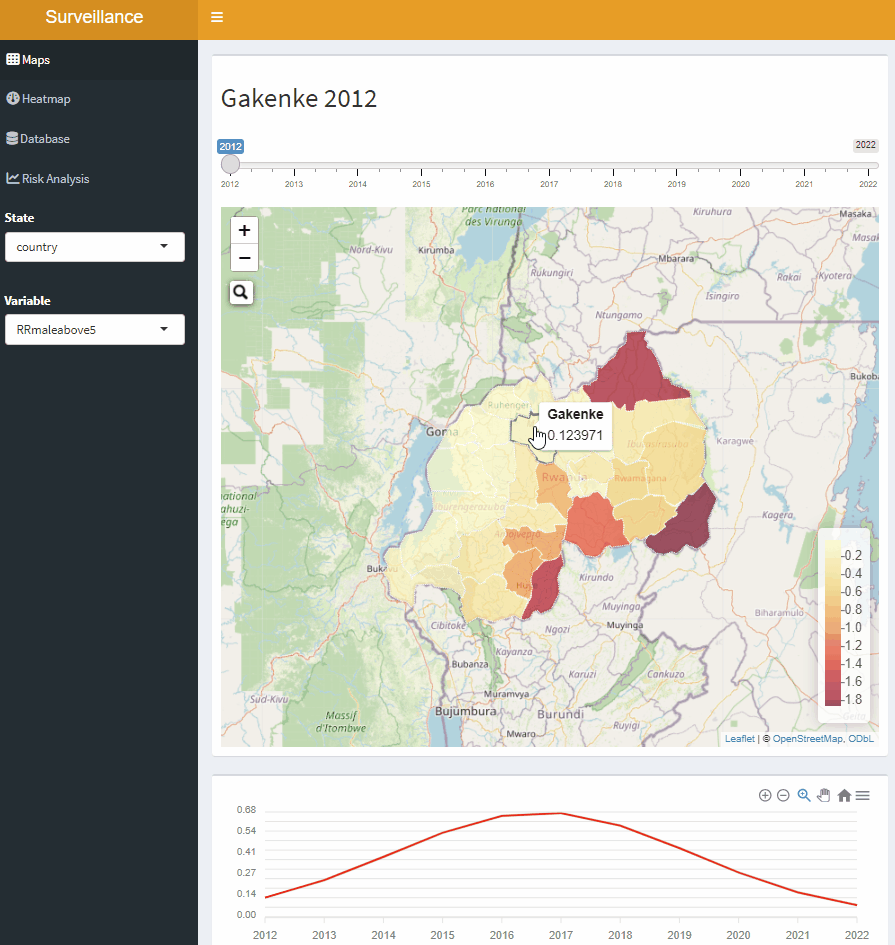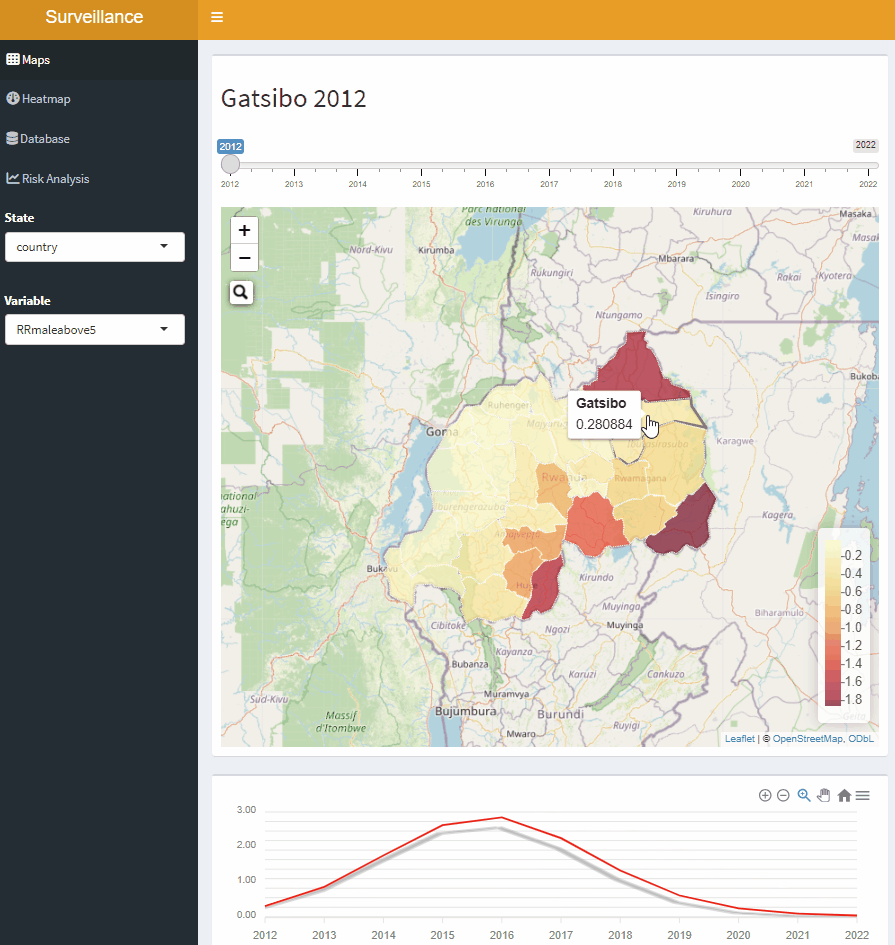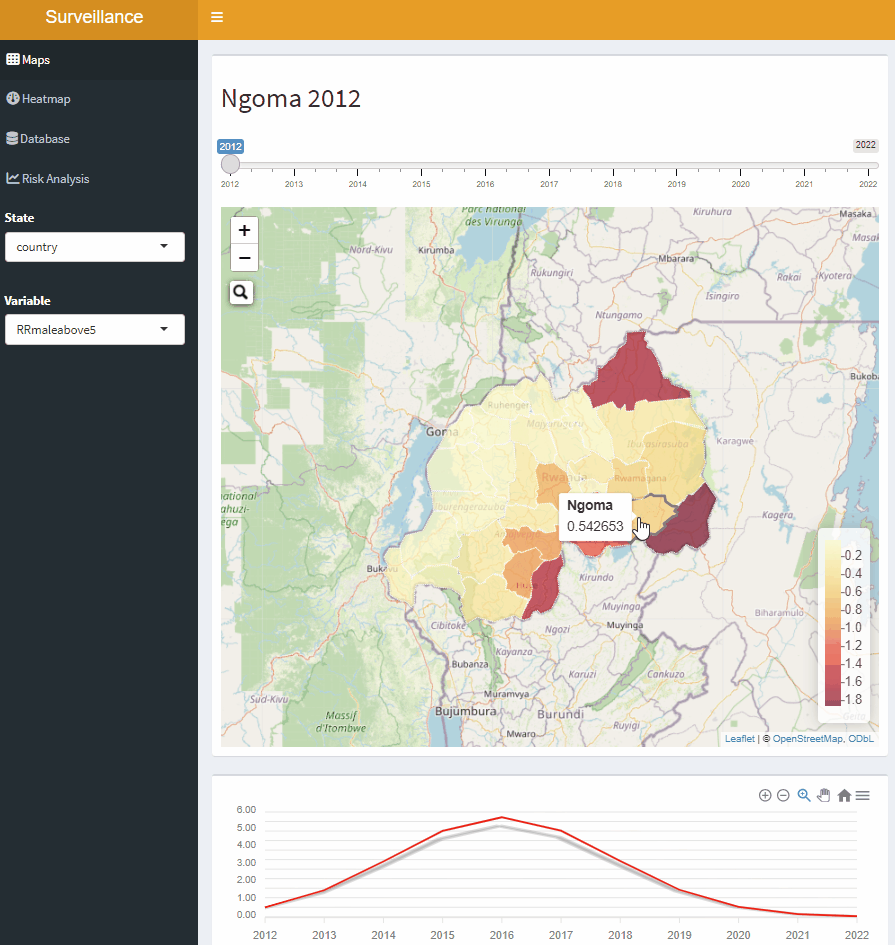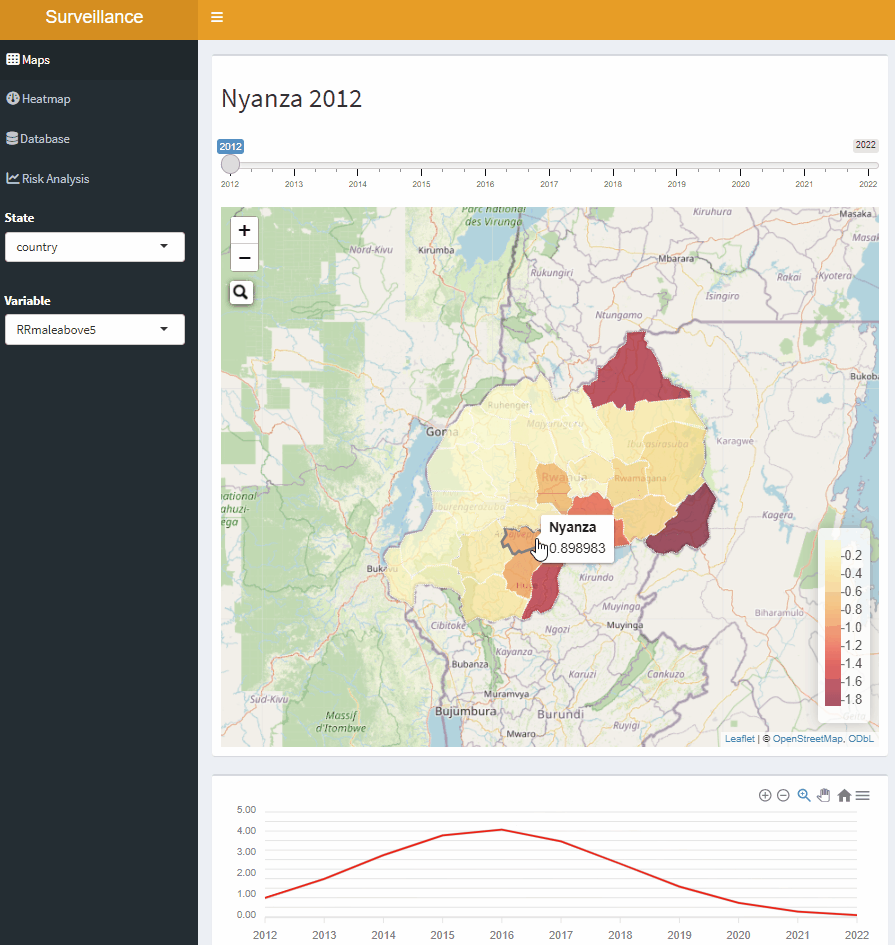
Interactive mapping tool for malaria risk in Rwanda, 2012-2022

Capacity Building
Capacity Building
Educational materials that impact learning on a large scale including my books. Provide training courses around the world to epidemiologists, public health professionals, researchers and university students


Capacity Building
Courses equip researchers on methods and tools to quantify disease burden, understand geographic and temporal patterns, identify risk factors, and measure inequalities between populations
They also show how to easily turn analyses into visually informative and interactive reports and dashboards that facilitate the communication of insights to collaborators and policymakers

Conclusions
Conclusions
Thank you!

|

|

|

|

|

|