Species Distribution Modeling using Spatial Point Processes: a Case Study of Sloths in Costa Rica
Paula Moraga
Materials based on the book Geospatial Health Data (2019, Chapman & Hall/CRC)
http://www.paulamoraga.com/book-geospatial
1 Abstract
Species distribution models are widely used in ecology for conservation management of species and their environments. This paper demonstrates how to fit a log-Gaussian Cox process model to predict the intensity of sloth occurrence in Costa Rica, and assess the effect of climatic factors on spatial patterns using the R-INLA package. Species occurrence data are retrieved using spocc, and spatial climatic variables are obtained with raster. Spatial data and results are manipulated and visualized by means of several packages such as raster and tmap. This tutorial provides an accessible illustration of spatial point process modeling that can be used to analyze data that arise in a wide range of fields including ecology, epidemiology and the environment.
A version of this tutorial appears in Moraga, P. Species Distribution Modeling using Spatial Point Processes: a Case Study of Sloth Occurrence in Costa Rica. The R Journal, 12(2):293-310, 2020.
2 Introduction
Species distribution models are widely used in ecology to predict and understand spatial patterns, assess the influence of climatic and environmental factors on species occurrence, and identify rare and endangered species. These models are crucial for the development of appropriate strategies that help protect species and the environments where they live.
In this paper, we demonstrate how to formulate spatial point processes for species distribution modeling and how to fit them with the R-INLA package (Rue, Martino, and Chopin 2009). Point processes are stochastic models that describe the locations of events of interest and possibly some additional information such as marks that inform about different types of events (Diggle 2013; Moraga and Montes 2011). These models can be used to identify patterns in the distribution of the observed locations, estimate the intensity of events (i.e., mean number of events per unit area), and learn about the correlation between the locations and spatial covariates.
The simplest theoretical point process model is the homogeneous Poisson process. This process satisfies two conditions. First, the number of events in any region \(A\) follows a Poisson distribution with mean \(\lambda |A|\), where \(\lambda\) is a constant value denoting the intensity and \(|A|\) is the area of region \(A\). And second, the number of events in disjoint regions are independent. Thus, if a point pattern arises as a realization of an homogeneous Poisson process, an event is equally likely to occur at any location within the study region, regardless of the locations of other events.
In many situations, the homogeneous Poisson process is too restrictive. A more interesting point process model is the log-Gaussian Cox process which is typically used to model phenomena that are environmentally driven (Diggle et al. 2013). A log-Gaussian Cox process is a Poisson process with a varying intensity which is itself a stochastic process of the form \(\Lambda(s) = exp(Z(s))\) where \(Z = \{Z(s): s \in \mathbb{R}^2\}\) is a Gaussian process. Then, conditional on \(\Lambda(s)\), the point process is a Poisson process with intensity \(\Lambda(s)\). This implies that the number of events in any region \(A\) is Poisson distributed with mean \(\int_A \Lambda(s)ds\), and the locations of events are an independent random sample from the distribution on \(A\) with probability density proportional to \(\Lambda(s)\). The log-Gaussian Cox process model can also be easily extended to include spatial explanatory variables providing a flexible approach for describing and predicting a wide range of spatial phenomena.
In this paper, we formulate and fit a log-Gaussian Cox process model for sloth occurrence data in Costa Rica that incorporates spatial covariates that can influence the occurrence of sloths, as well as random effects to model unexplained variability. The model allows to estimate the intensity of the process that generates the data, understand the overall spatial distribution, and assess factors that can affect spatial patterns. This information can be used by decision-makers to develop and implement conservation management strategies.
The rest of the paper is organized as follows. First, we show how to retrieve sloth occurrence data using the spocc package (Chamberlain 2018) and spatial climatic variables using the raster package (Hijmans 2019). Then, we detail how to formulate the log-Gaussian Cox process and how to use R-INLA to fit the model. Then, we inspect the results and show how to obtain the estimates of the model parameters, and how to create create maps of the intensity of the predicted process. Finally, the conclusions are presented.
3 Sloth occurrence data
Sloths are tree-living mammals found in the tropical rain forests of Central and South America. They have an exceptionally low metabolic rate and are noted for slowness of movement. There are six sloth species and two types, two-toed and three-toed sloths. Here, we use the R package spocc (Chamberlain 2018) to retrieve occurrence data of the three-toed brown-throated sloth in Costa Rica. spocc provides functionality for retrieving and combining species occurrence data from many data sources such as from the Global Biodiversity Information Facility (GBIF) and th Atlas of Living Australia (ALA).
We use the occ() function from spocc to retrieve the locations of brown-throated sloth in Costa Rica recorded between 2000 and 2019 from GBIF.
In the function, we specify arguments query with the species scientific name (Bradypus variegatus), from with the name of the database (GBIF), and date with the start and end dates (2000-01-01 to 2019-12-31).
We also specify we wish to retrieve occurrences in Costa Rica by setting gbifopts to a named list with
country equal to the 2-letter code of Costa Rica (CR).
Moreover, we only retrieve occurrence data that have coordinates by setting has_coords = TRUE, and specify limit equal to 1000 to retrieve a maximum of 1000 occurrences.
library('spocc')
df <- occ(query = 'Bradypus variegatus', from = 'gbif',
date = c("2000-01-01", "2019-12-31"),
gbifopts = list(country = "CR"),
has_coords = TRUE, limit = 1000)The output of occ() is of class occdat and has slots for each of data sources. We can see the slots names by typing names(df).
names(df)## [1] "gbif" "bison" "inat" "ebird" "vertnet" "idigbio" "obis"
## [8] "ala"In this case, since we only retrieve data from GBIF, the only slot with data is df$gbif while the others are empty.
df$gbif contains information about the species occurrence and also other details about the retrieval process.
We can use the occ2df() function to combine the output of occ() and create a single data frame with the most relevant information for our analysis, namely, the species name, the decimal degree longitude and latitude values, the data provider, and the dates and keys of the occurrence records.
d <- occ2df(df)A summary of the data can be seen with summary(d). We observe the data contain 886 locations of sloths occurred between 2000-01-24 and 2019-12-30.
summary(d)## name longitude latitude prov
## Length:886 Min. :-85.52 Min. : 8.340 Length:886
## Class :character 1st Qu.:-84.14 1st Qu.: 9.390 Class :character
## Mode :character Median :-84.01 Median : 9.826 Mode :character
## Mean :-83.87 Mean : 9.909
## 3rd Qu.:-83.51 3rd Qu.:10.455
## Max. :-82.62 Max. :11.038
## date key
## Min. :2000-01-24 Length:886
## 1st Qu.:2013-08-05 Class :character
## Median :2017-03-13 Mode :character
## Mean :2015-10-04
## 3rd Qu.:2018-12-27
## Max. :2019-12-30We can visualize the locations of sloths retrieved in Costa Rica using several mapping packages such as tmap (Tennekes 2018), ggplot2 (Wickham 2016), leaflet (Cheng, Karambelkar, and Xie 2018), and mapview (Appelhans et al. 2019). Here we choose to create maps using tmap.
First, we use the SpatialPoints() function from the sp (Pebesma and Bivand 2005) package to create a SpatialPoints object called dpts with the coordinates of the sloth locations.
library(sp)
dpts <- SpatialPoints(d[, c("longitude", "latitude")])Then we create the map plotting the locations of dpts. tmap allows to create both static and interactive maps by using tmap_mode("plot") or tmap_mode("view"), respectively. Here, we create an interactive map using use a basemap given by the OpenStreetmap provider, and plot the the sloth locations with tm_shape(dpts) + tm_dots().
library(tmap)tmap_mode("view")
tm_basemap() + tm_shape(dpts) + tm_dots()The map created shows an inhomogeneous pattern of sloths with concentrations in several locations of Costa Rica. We will use a log-Gaussian Cox point process model to predict the intensity of the process that generates the sloth locations and assess the potential effect that climatic variables have on the occurrence pattern.
4 Spatial climatic covariates
In the model, we include a spatial explanatory variable that can potentially affect sloth occurrence.
Specifically, we include a variable that denotes annual minimum temperature observed in the study region.
This variable can be obtained using the raster package (Hijmans 2019) from the WorldClim database (http://www.worldclim.org/bioclim).
We use the getData() function of the raster package by specifying the name of the database ("worldclim"),
the variable name ("tmin"), and a resolution of 10 minutes of a degree ("10").
getData() returns a RasterStack with minimum temperature observations for each month.
Values are degrees centigrade multiplied by 10.
We average the values of the RasterStack and compute a raster that represents annual average minimum temperature.
library(raster)
rmonth <- getData(name = "worldclim", var = "tmin", res = 10)
plot(rmonth)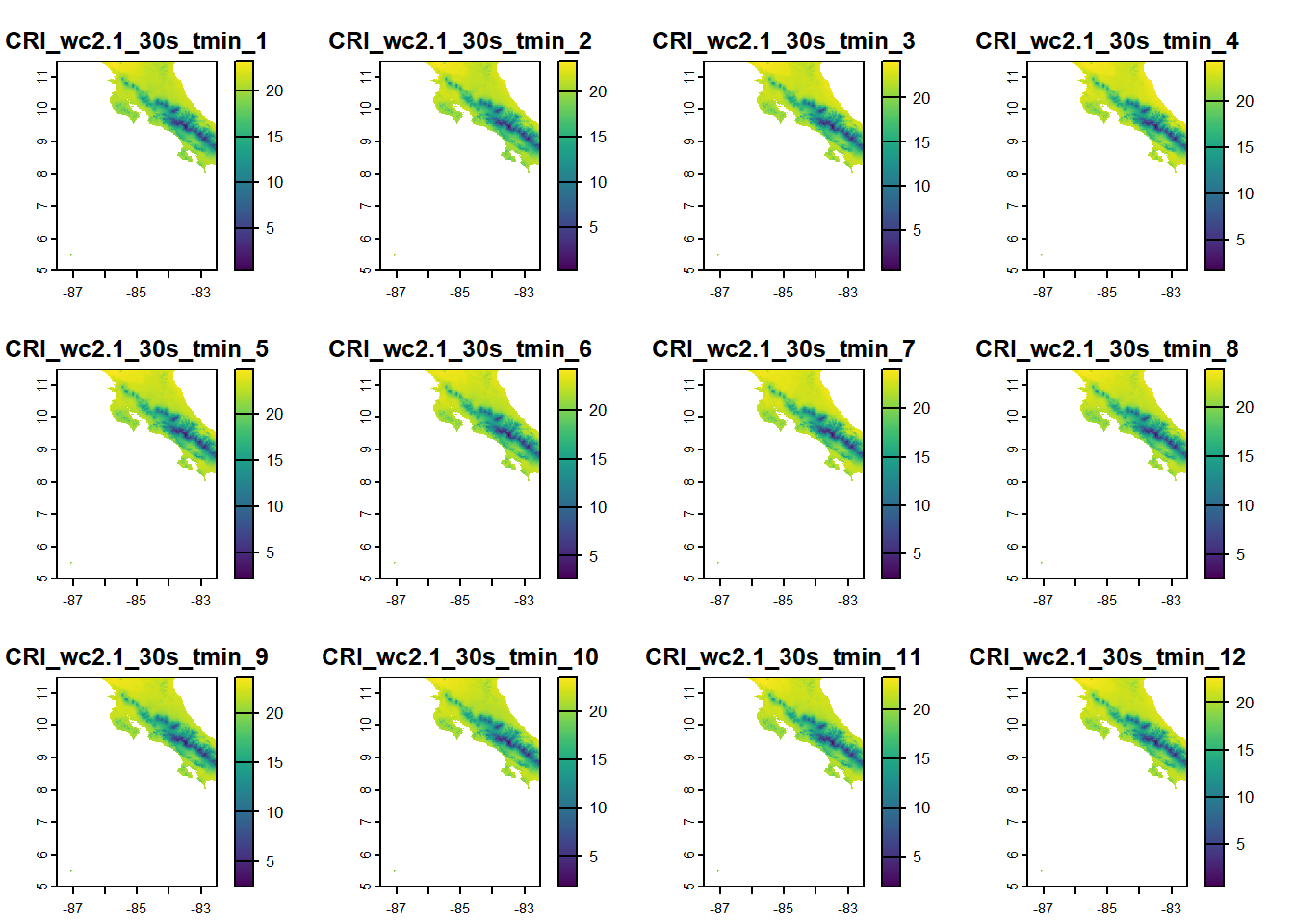
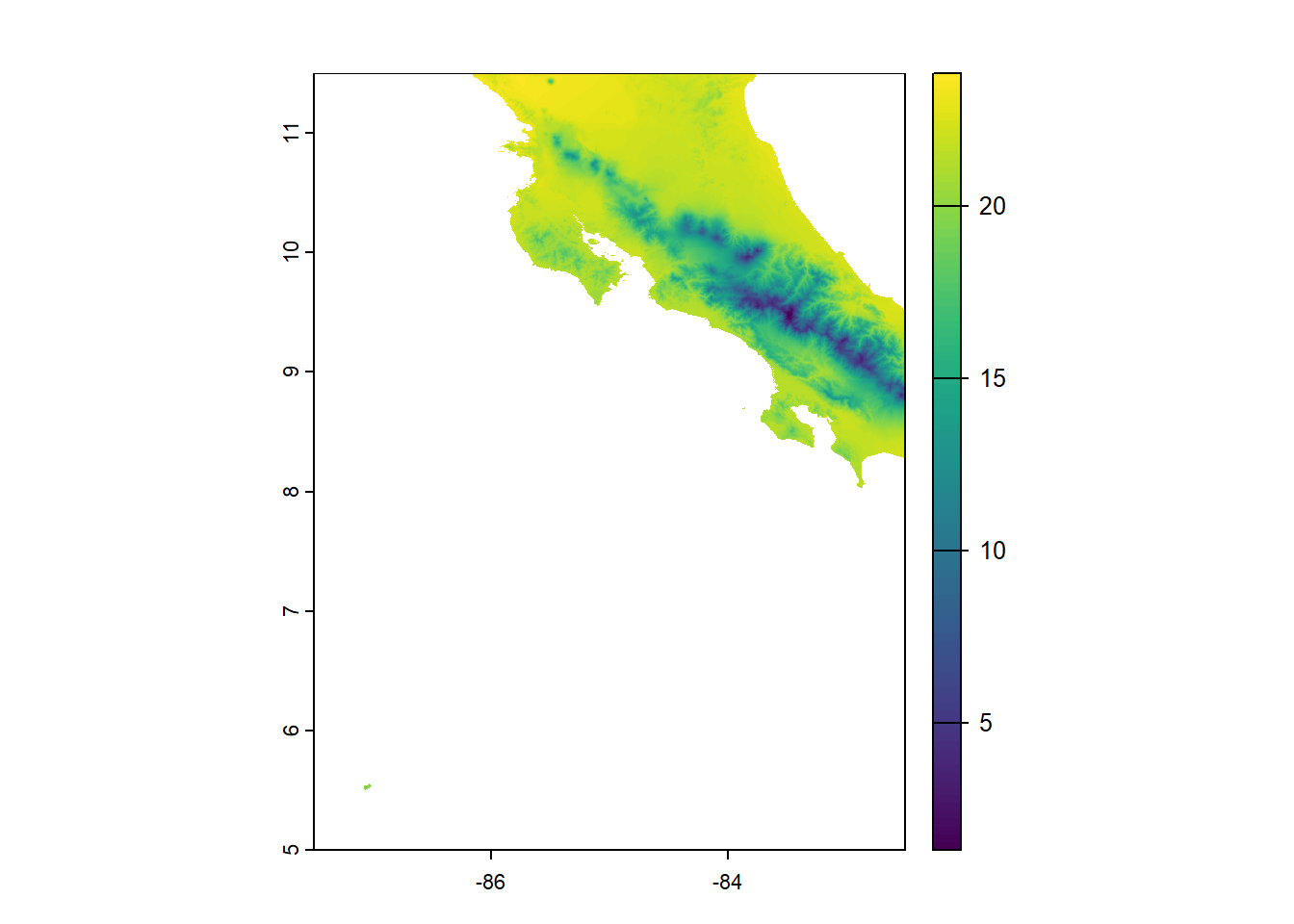
rcov <- mean(rmonth)
plot(rcov)
5 Implementing and fitting the spatial point process model
5.1 Log-Gaussian Cox process model
We assume that the spatial point pattern of sloth locations in Costa Rica, \(\{s_i: i=1, \ldots, n\}\), has been generated as a realization of a log-Gaussian Cox process with intensity given by \(\Lambda(s)= exp(\eta(s))\).
This model can be easily fitted by approximating it by a latent Gaussian model by means of a gridding approach (Illian et al. 2012).
First, we discretize the study region into a grid with \(n_1 \times n_2 = N\) cells \(\{s_{ij}\}\), \(i=1,\ldots,n_1,\), \(j=1,\ldots,n_2\).
In the log-Gaussian Cox process, the mean number of events in cell \(s_{ij}\) is given by the integral of the intensity over the cell,
\(\Lambda_{ij}=\int_{s_{ij}} exp(\eta(s))ds\), and
this integral can be approximated by
\(\Lambda_{ij} \approx |s_{ij}| exp(\eta_{ij})\),
where \(|s_{ij}|\) is the area of the cell \(s_{ij}\).
Then, conditional on the latent field \(\eta_{ij}\),
the observed number of locations in grid cell \(s_{ij}\),
\(y_{ij}\), are independent and Poisson distributed as follows:
\[y_{ij}|\eta_{ij} \sim Poisson(|s_{ij}| exp(\eta_{ij})).\]
In our example, we model the log-intensity of the Poisson process as
\[\eta_{ij} = \beta_0 + \beta_1 \times cov(s_{ij}) + f_s(s_{ij}) + f_u(s_{ij}).\]
Here \(\beta_0\) is the intercept,
\(cov(s_{ij})\) is the covariate at \(s_{ij}\), and
\(\beta_1\) is the coefficient of \(cov(s_{ij})\).
f_s() is a spatially structured random effect reflecting unexplained variability that can be specified as a second-order two-dimensional CAR-model on a regular lattice.
f_u() is a unstructured random effect reflecting independent variability in cell \(s_{ij}\).
5.2 Computational grid
In order to fit the model, we create a regular grid that covers the region of Costa Rica.
First, we obtain a map of Costa Rica using the ne_countries() function of the rnaturalearth package (South 2017). In the function we set type = "countries", country = "Costa Rica" and scale = "medium"(scale denotes the scale of map to return and possible options are small, medium and large).
library(rnaturalearth)
map <- ne_countries(type = "countries", country = "Costa Rica", scale = "medium")
plot(map)
Then, we create a raster tha covers Costa Rica using raster() where we provide the of map Costa Rica and set resolution = 0.1 to create cells with size of 0.1 decimal degrees.
This creates a raster with 31 \(\times\) 33 = 1023 cells, each having an area equal to 0.1\(^2\) decimal degrees\(^2\) (or 11.132 km\(^2\) at the equator).
resolution <- 0.1
r <- raster(map, resolution = resolution)
print(r)## class : RasterLayer
## dimensions : 31, 33, 1023 (nrow, ncol, ncell)
## resolution : 0.1, 0.1 (x, y)
## extent : -85.90801, -82.60801, 8.089453, 11.18945 (xmin, xmax, ymin, ymax)
## crs : +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0(nrow <- nrow(r))## [1] 31(ncol <- ncol(r))## [1] 33nrow*ncol## [1] 1023We initially set to 0 the values of all the grid cells by using r[] <- 0.
Then, we use cellFromXY() to obtain the number of sloths in each of the cells where sloths occur, and assign these counts to each of the cells of the raster.
r[] <- 0
tab <- table(cellFromXY(r, dpts))
tab##
## 37 38 39 45 70 72 78 79 105 106 111 113 141 142 146 175 179 180 189 209
## 1 1 1 5 1 1 12 1 1 1 4 1 10 2 2 2 2 3 9 1
## 210 211 218 222 223 243 244 245 246 248 249 250 251 253 255 256 257 275 276 277
## 1 10 2 41 37 14 47 3 2 1 14 34 42 2 2 2 1 3 1 2
## 278 280 288 290 308 312 316 317 318 319 320 321 322 324 347 349 350 352 357 372
## 12 1 1 4 1 2 1 2 12 16 1 3 1 1 1 1 15 1 1 1
## 381 382 389 391 392 415 419 424 425 443 452 453 459 460 476 481 484 493 494 503
## 1 2 16 4 2 10 3 1 2 1 1 1 3 1 1 1 11 45 2 1
## 512 518 523 527 528 541 542 548 578 579 580 612 615 616 617 646 648 649 650 653
## 1 3 1 30 38 1 1 1 2 78 2 126 1 3 1 1 28 2 1 1
## 682 683 685 687 716 782 783 815 848 850 852 882 883 915 917 918 919 950 952
## 4 1 1 1 1 5 3 9 4 1 1 4 2 8 2 5 1 1 1r[as.numeric(names(tab))] <- tab
plot(r)
Finally, we convert the raster r to a SpatialPolygonsDataFrame object called grid using rasterToPolygons() .
This grid will be used to fit the model with the R-INLA package.
grid <- rasterToPolygons(r)5.3 Data
Now, we include in the SpatialPolygonsDataFrame grid the data needed for modeling. Since the spatial model that will be used in R-INLA assumes data are sorted by columns, we first transpose grid. Then, we add the following variables:
idwith the id of the cells,Ywith the number of sloths, andcellareawith the cell areas.
grid <- grid[as.vector(t(matrix(1:nrow(grid), nrow = ncol, ncol = nrow))), ]
grid$id <- 1:nrow(grid)
grid$Y <- grid$layer
grid$cellarea <- resolution*resolutionWe also add a variable cov with the value of the covariate in each of the cells obtained with the extract() function of raster.
grid$cov <- extract(rcov, coordinates(grid))Finally, we delete the cells of grid that fall outside Costa Rica.
First, we use raster::intersect() to know which cells fall within the map, and then subset these cells in the grid object.
plot(grid)
gridmap <- raster::intersect(grid, map)
grid <- grid[grid$id %in% gridmap$id, ]
plot(grid)
A summary of the data can be seen as follows:
summary(grid)## Object of class SpatialPolygonsDataFrame
## Coordinates:
## min max
## x -85.908008 -82.60801
## y 8.089453 11.18945
## Is projected: FALSE
## proj4string :
## [+proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0]
## Data attributes:
## layer id Y cellarea
## Min. : 0.000 Min. : 3.0 Min. : 0.000 Min. :0.01
## 1st Qu.: 0.000 1st Qu.: 291.5 1st Qu.: 0.000 1st Qu.:0.01
## Median : 0.000 Median : 566.0 Median : 0.000 Median :0.01
## Mean : 1.728 Mean : 533.1 Mean : 1.728 Mean :0.01
## 3rd Qu.: 0.000 3rd Qu.: 762.5 3rd Qu.: 0.000 3rd Qu.:0.01
## Max. :126.000 Max. :1009.0 Max. :126.000 Max. :0.01
##
## cov
## Min. : 78.0
## 1st Qu.:176.7
## Median :202.4
## Mean :189.0
## 3rd Qu.:211.2
## Max. :223.2
## NA's :2We observe that the covariate has 2 missing values. We decide to impute them with a simple approach where we set these values equal to the values of the cells next to them.
indNA <- which(is.na(grid$cov))
indNA## [1] 6 220grid$cov[indNA] <- grid$cov[indNA+1]We use tmap to create maps of the number of sloths and the covariate values in each of the cells.
In the maps, we plot the border of grid that we obtain with the gUnaryUnion() function of the rgeos package.
library(rgeos)
gridborder <- gUnaryUnion(grid)We use tm_facets(ncol = 2) to display the maps in the same row and two columns, and tm_legend() to put the legends in the left-bottom corner of the plots.
tmap_mode("plot")
tm_shape(grid) +
tm_polygons(col = c("Y", "cov"), border.col = "transparent") +
tm_shape(gridborder) + tm_borders() +
tm_facets(ncol = 2) + tm_legend(legend.position = c("left", "bottom"))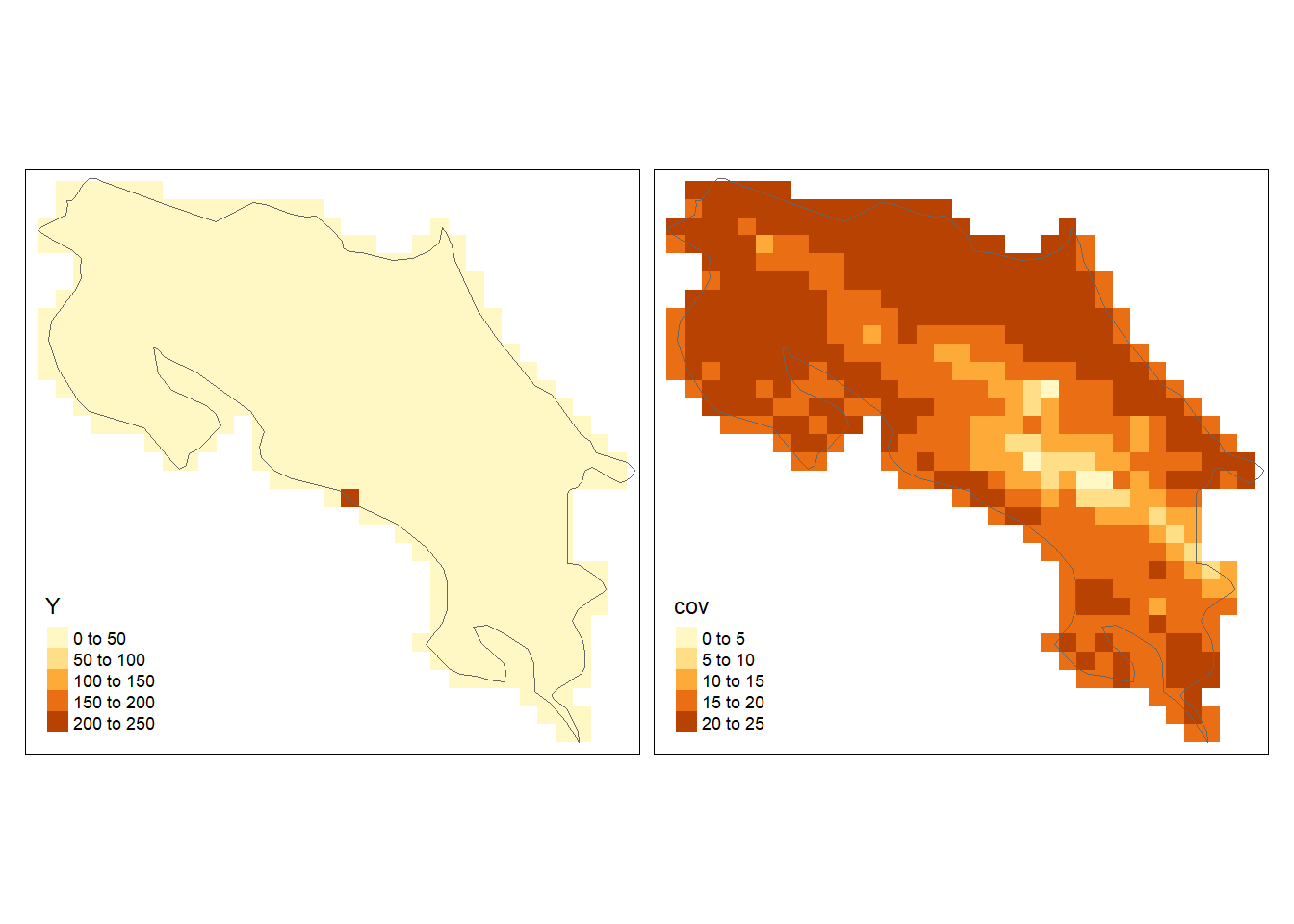
5.4 Fitting the model using INLA
We fit the log-Gaussian Cox process model to the sloths data using the R-INLA package. This package implements the integrated nested Laplace approximation (INLA) approach that permits to perform approximate Bayesian inference in latent Gaussian models (Rue, Martino, and Chopin 2009; Moraga. 2019).
R-INLA is not on CRAN because it uses some external C libraries that make difficult to build the binaries. Therefore, when installing the package, we need to specify the URL of the R-INLA repository as follows:
install.packages("INLA",
repos = "https://inla.r-inla-download.org/R/stable", dep = TRUE)To fit the model in INLA we need to specify a formula with the linear predictor, and then call the inla() function providing the formula, the family, the data, and other options.
The formula is written by writing the outcome variable,
then the ~ symbol, and then the fixed and random effects separated by + symbols.
By default, the formula includes an intercept.
The outcome variable is Y (the number of occurrences in each cell) and the covariate is cov.
The random effects are specified with the f() function where the first argument is an index vector specifying which elements of the random effect apply to each observation, and the other arguments are the model name and other options.
In the formula, different random effects need to have different indices vectors.
We use grid$id for the spatially structured effect,
and create an index vector grid$id2 with the same values as grid$id
for the unstructured random effect.
The spatially structured random effect with ICAR(2) is specified with the index vector id, the model name that corresponds to ICAR(2) ("rw2d"), and the number of rows (nrow) and columns (ncol) of the regular lattice.
The unstructured random effect is specified with the index vector id2 and the model name "iid".
Finally, we call inla() where we provide the formula, the family (poisson) and the data (grid@data). We write E = cellarea to denote that the expected values in each of the cells are in the variable cellarea of the data.
We also write control.predictor = list(compute = TRUE) to compute the marginal densities for the linear predictor.
library(INLA)
grid$id2 <- grid$id
formula <- Y ~ 1 + cov +
f(id, model="rw2d", nrow = nrow, ncol = ncol) +
f(id2, model="iid")
res <- inla(formula, family = "poisson", data = grid@data,
E = cellarea, control.predictor = list(compute = TRUE))5.5 Results
The execution of inla() returns an object res that contains information about the fitted model including the posterior marginals of the parameters and the intemsity values of the spatial process.
We can see a summary of the results as follows.
summary(res)##
## Call:
## c("inla(formula = formula, family = \"poisson\", data = grid@data, ", "
## E = cellarea, control.predictor = list(compute = TRUE))" )
## Time used:
## Pre = 0.584, Running = 6.99, Post = 0.105, Total = 7.68
## Fixed effects:
## mean sd 0.025quant 0.5quant 0.975quant mode kld
## (Intercept) -1.883 2.467 -6.893 -1.832 2.835 -1.734 0
## cov 0.018 0.010 -0.001 0.018 0.037 0.017 0
##
## Random effects:
## Name Model
## id Random walk 2D
## id2 IID model
##
## Model hyperparameters:
## mean sd 0.025quant 0.5quant 0.975quant mode
## Precision for id 0.376 0.174 0.143 0.342 0.811 0.282
## Precision for id2 0.303 0.063 0.197 0.298 0.444 0.286
##
## Expected number of effective parameters(stdev): 206.78(6.94)
## Number of equivalent replicates : 2.47
##
## Marginal log-Likelihood: -1668.02
## Posterior marginals for the linear predictor and
## the fitted values are computedThe intercept \(\hat \beta_0=\) -1.883 with a 95% credible interval equal to
(-6.893, 2.835),
the covariate minimum temperature has a positive
effect on the intensity of the process with a posterior mean \(\hat \beta_1=\) 0.018 with a 95% credible interval equal to
(-0.001, 0.037).
We can plot the posterior distribution of the coefficient of the covariate \(\hat \beta_1\) with ggplot2.
First, we calculate a smoothing of the marginal distribution of the coefficient with inla.smarginal() and then call ggplot() specifying the data frame with the marginal values.
library(ggplot2)
marginal <- inla.smarginal(res$marginals.fixed$cov)
marginal <- data.frame(marginal)
ggplot(marginal, aes(x = x, y = y)) + geom_line() +
labs(x = expression(beta[1]), y = "Density") +
geom_vline(xintercept = 0, col = "black") + theme_bw()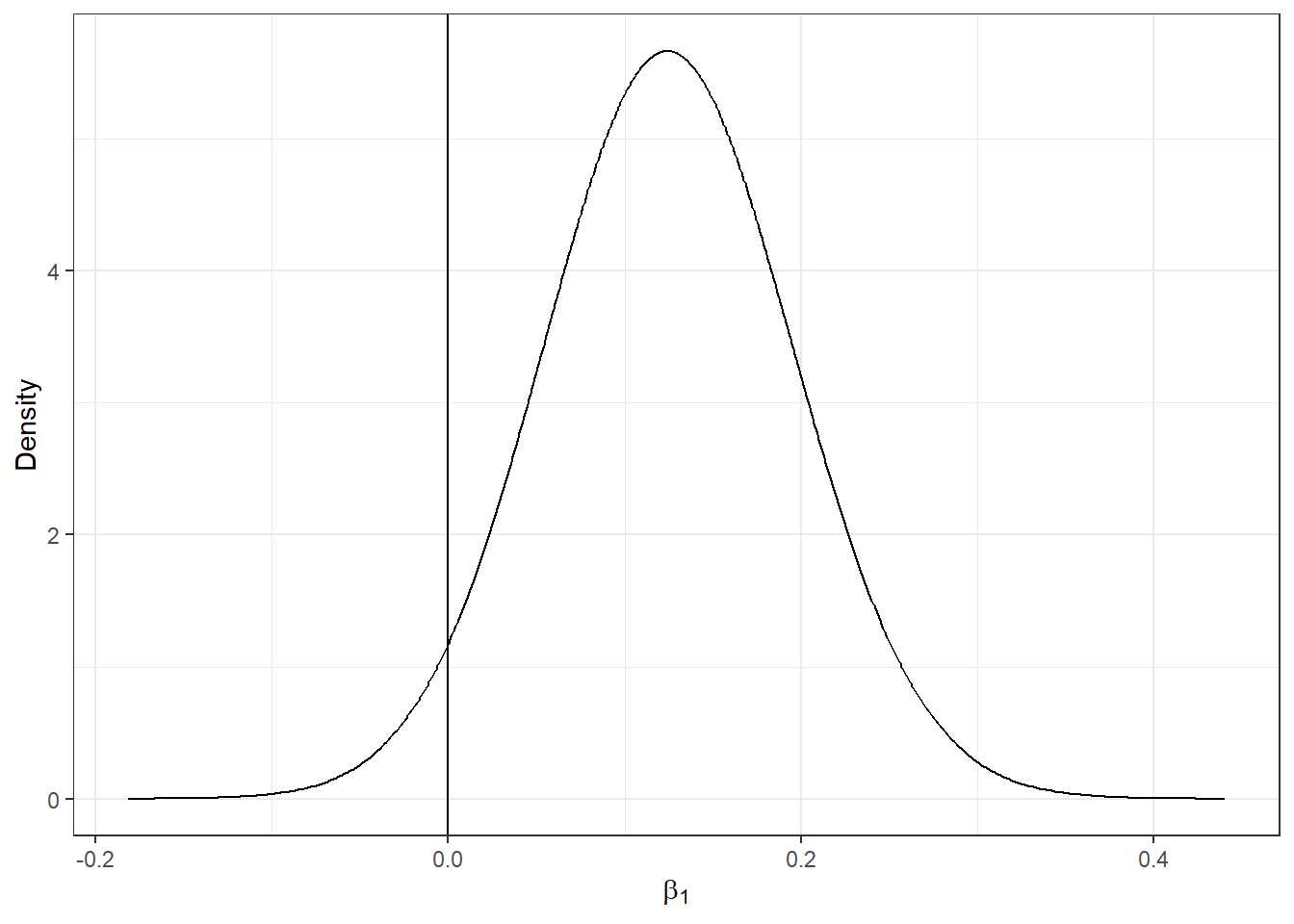
The estimated spatially structured effect can be retrieved with
res$summary.random$id. This contains 1023 elements that correspond to the number of cells in the regular lattice. We can add to grid the posterior mean of the spatial effect corresponding to each of the cells in Costa Rica as follows.
nrow(res$summary.random$id)## [1] 1023grid$respa <- res$summary.random$id[grid$id, "mean"]We can also obtain the posterior mean of the unstructured random effect.
grid$reiid <- res$summary.random$id2[, "mean"]Then we can create maps of the random effects with tmap.
tm_shape(grid) +
tm_polygons(col = c("respa", "reiid"), style = "cont", border.col = "transparent") +
tm_shape(gridborder) + tm_borders() +
tm_facets(ncol = 2) + tm_legend(legend.position = c("left", "bottom"))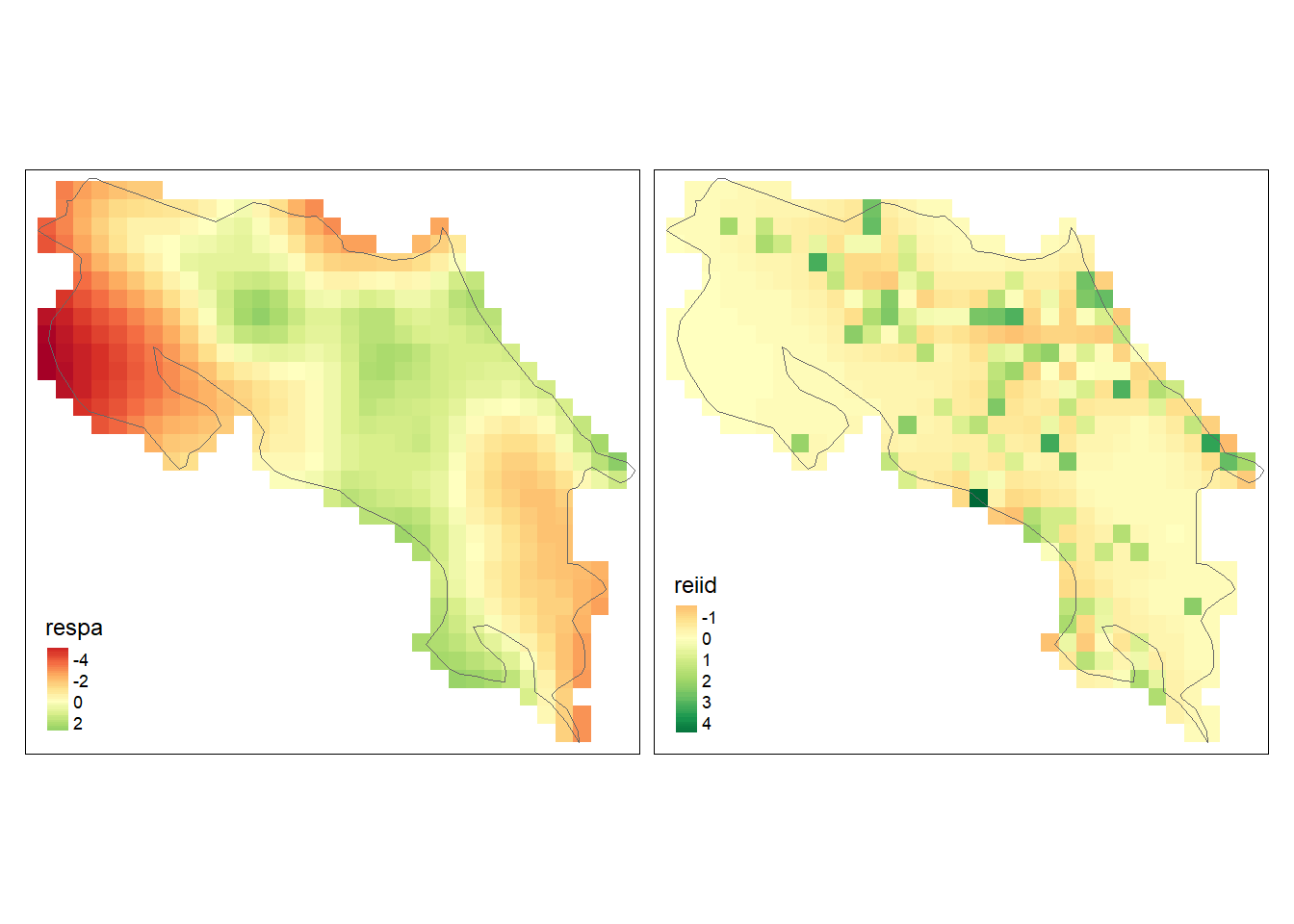
We observe a non-constant pattern of the spatial structured random effect suggesting that the intensity of the process that generates the sloth locations may be affected by other spatial factors that have not been considered in the model. Moreover, the unstructured random effect shows several locations with high values that modify the intensity of the process in individual cells independently of the rest.
The mean and quantiles of the predicted intensity (mean number of events per unit area) in each of the grid cells are in res$summary.fitted.values.
In the object grid, we add a variable NE with the mean number of events of each cell by assigning the predicted intensity multiplied by the cell areas. We also add variables LL and UL with the lower and upper limits of 95% credible intervals for the number of events by assigning quantiles 0.025 and 0.975 multiplied by the cell areas.
cellarea <- resolution*resolution
grid$NE <- res$summary.fitted.values[, "mean"] * cellarea
grid$LL <- res$summary.fitted.values[, "0.025quant"] * cellarea
grid$UL <- res$summary.fitted.values[, "0.975quant"] * cellarea
summary(grid)## Object of class SpatialPolygonsDataFrame
## Coordinates:
## min max
## x -85.908008 -82.60801
## y 8.089453 11.18945
## Is projected: FALSE
## proj4string :
## [+proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0]
## Data attributes:
## layer id Y cellarea
## Min. : 0.000 Min. : 3.0 Min. : 0.000 Min. :0.01
## 1st Qu.: 0.000 1st Qu.: 291.5 1st Qu.: 0.000 1st Qu.:0.01
## Median : 0.000 Median : 566.0 Median : 0.000 Median :0.01
## Mean : 1.728 Mean : 533.1 Mean : 1.728 Mean :0.01
## 3rd Qu.: 0.000 3rd Qu.: 762.5 3rd Qu.: 0.000 3rd Qu.:0.01
## Max. :126.000 Max. :1009.0 Max. :126.000 Max. :0.01
## cov id2 respa reiid
## Min. : 78.0 Min. : 3.0 Min. :-8.6147 Min. :-1.659505
## 1st Qu.:176.8 1st Qu.: 291.5 1st Qu.:-1.7385 1st Qu.:-0.286823
## Median :202.4 Median : 566.0 Median : 0.3852 Median :-0.040692
## Mean :189.1 Mean : 533.1 Mean :-0.2140 Mean : 0.163876
## 3rd Qu.:211.2 3rd Qu.: 762.5 3rd Qu.: 1.8194 3rd Qu.: 0.008275
## Max. :223.2 Max. :1009.0 Max. : 4.1319 Max. : 4.158909
## NE LL UL
## Min. : 0.00276 Min. : 0.00000 Min. : 0.01709
## 1st Qu.: 0.05656 1st Qu.: 0.00011 1st Qu.: 0.39007
## Median : 0.18693 Median : 0.00142 Median : 1.13502
## Mean : 1.84017 Mean : 1.02509 Mean : 3.50935
## 3rd Qu.: 0.58434 3rd Qu.: 0.01521 3rd Qu.: 2.59222
## Max. :125.37226 Max. :104.33427 Max. :148.13776We use tmap to create maps with the mean and lower and upper limits of 95% credible intervals for the number of events.
We plot the three maps with a common legend that has breaks from 0 to the maximum number of cases in grid$UL.
tm_shape(grid) +
tm_polygons(col = c("NE", "LL", "UL"),
style = 'fixed', border.col = "transparent",
breaks = c(0, 10, 50, 100, ceiling(max(grid$UL)))) +
tm_shape(gridborder) + tm_borders() +
tm_facets(ncol = 3) + tm_legend(legend.position = c("left", "bottom"))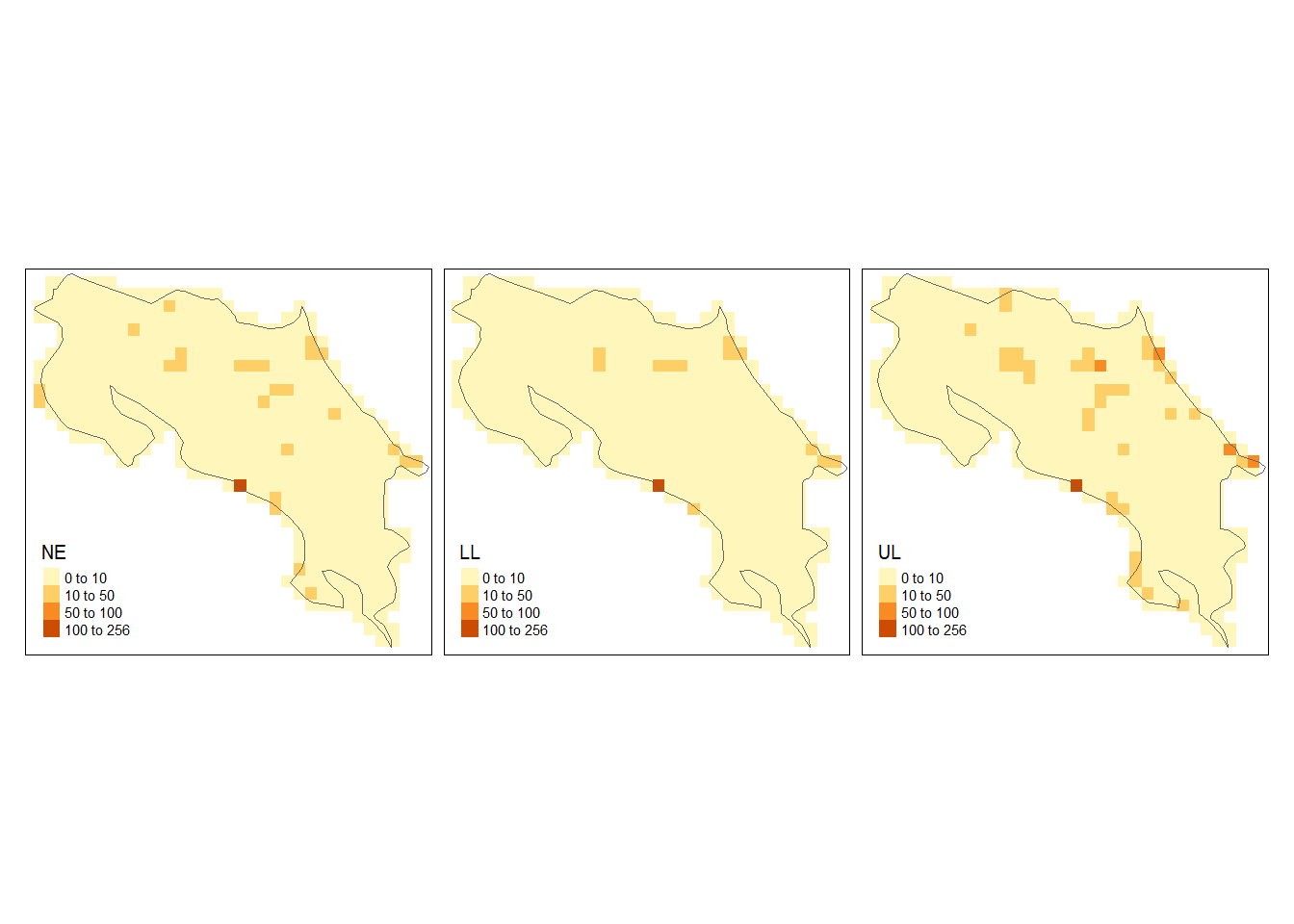 
We observe that overall, the intensity of sloth occurrence is low, with less than 10 sloths in each of the cells. There are also some locations of high sloth intensity in the west and east coasts and the north of Costa Rica. The maps with the lower and upper limits of 95% credible intervals denote the uncertainty of these predictions. These maps inform about the spatial patterns in the period where the data were collected. In addition, maps of the sloth numbers over time can also be produced using spatio-temporal point process models and this will help understand spatio-temporal patterns. These results can be useful for decision-makers to identify areas of interest for conservation management strategies.
6 Discussion
Species distribution models are widely used in ecology for conservation management of species and their environments. In this paper, we have described a log-Gaussian Cox process that can be used to model species occurrence data, and assess the effect of spatial explanatory variables, and how to fit the model using the R-INLA package. We have illustrated the modeling approach using sloth occurrence data in Costa Rica that retrieved from the Global Biodiversity Information Facility database (GBIF) using the spocc package and a spatial climatic variable obtained with the raster package. We have also shown how to examine and interpret the results including the estimates of the parameters and the intensity of the process, and how to create maps of variables of interest using the tmap package.
The objective of this paper is to illustrate how to analyze species occurrence data using spatial point process models and cutting-edge statistical techniques in R. Therefore, we have ignored the data collection methods and have assumed that the spatial pattern analyzed is a realization of the true underlying process that generates the locations. In real investigations, however, it is important to understand the sampling mechanisms, and assess potential biases in the data such as overrepresentation of certain areas that can invalidate inferences. Ideally, we would use data that have been obtained using well-defined sampling schemes. Alternatively, we would need to develop models that adjust for data biases to produce meaningful results. Moreover, expert knowledge is crucial to be able to develop appropriate models that include important predictive covariates and random effects that account for different types of variability.
To conclude, this paper provides an accessible illustration of spatial point process models and computational approaches that can help non-statisticians analyze spatial point patterns using R. We have shown how to use these approaches in the context of species distribution modeling, but they are also useful to analyze spatial data that arise in many other fields such as epidemiology or the environment.
This work by Paula Moraga is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
7 References
Moraga, P. Species Distribution Modeling using Spatial Point Processes: a Case Study of Sloth Occurrence in Costa Rica. The R Journal, 12(2):293-310, 2020 https://journal.r-project.org/archive/2021/RJ-2021-017/RJ-2021-017.pdf
Moraga, P. (2019). Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny. Chapman & Hall/CRC Biostatistics Series, http://www.paulamoraga.com/book-geospatial