library(survival)
tt <- c(1,3,2,3,2,5,6,3)
status <- c(1,1,0,0,1,0,0,1)
# status indicates whether the outcome was observed (status = 1)
# or that survival time was censored (status = 0)
fit <- survfit(Surv(tt, status) ~ 1)
summary(fit)
plot(fit)44 Survival
44.1 Survival
Determine the survival and density functions for the survival random variable with the following hazard function: \[h(x) = \frac{2x}{1+x^2}\]
Survival. Solutions
\[H(x) = \int_0^x h(t)dt = \int_0^x \frac{2t}{1+t^2}dt = log(1+t^2)|_0^x = log(1+x^2)\] \[S(x) = exp[-H(x)]=exp[-log(1+x^2)]=\frac{1}{1+x^2}\] \[f(x)=h(x)S(x)=\frac{2x}{(1+x^2)^2}\]
44.2 Survival
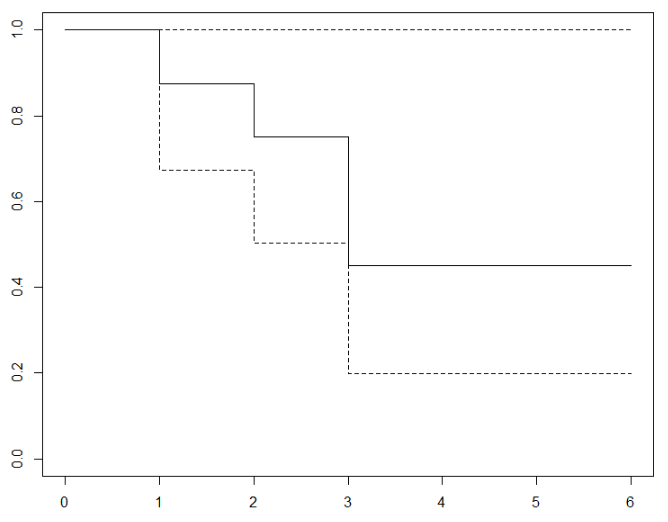
Consider a small study with 8 subjects. The event times were recorded as follows: \[1,3,2+,3+,2,5+,6+,3\] Here, “1” means the exact event time is 1. “2+” means the subject is censored at time 2 and its event time is greater than 2. Calculate the Kaplan-Meier estimates for the survival function \(S(x)\).
Make a plot of the survival function based on the estimates obtained.
Survival. Solutions
The Kaplan-Meier estimator of \(S(t) = P(T > t)\) is
\[\hat S(t) = \prod_{t_i \leq t} \left(1-\frac{d_i}{n_i}\right)\]
| \(t_i\) | \(d_i\) | \(n_i\) | \(\hat S(t_i)\) |
|---|---|---|---|
| 0 | 0 | 8 | 1 |
| 1 | 1 | 8 | (1-1/8)=7/8 |
| 2 | 1 | 7 | (1-1/8)(1-1/7)=3/4 |
| 3 | 2 | 5 | (1-1/8)(1-1/7)(1-2/5)=9/20 |
\[\hat S(t_{i}) = \hat S(t_{i-1}) \times \hat P(T > t_{i} | T \geq t_{i}) = \prod_{j=1}^i \hat P(T > t_{j} | T \geq t_{j})\]