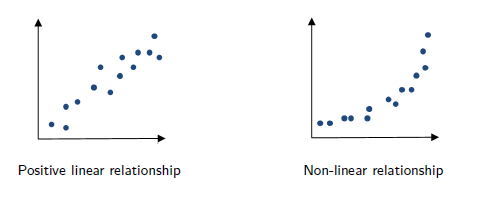
6 Introduction
6.1 Linear regression and correlation
A regression model describes the linear relationship between a continuous response variable \(Y\) and one or more explanatory variables \(X_1, X_2, \dots, X_p\)
In simple linear regression there is one explanatory variable \[\hat Y = \hat \beta_0 + \hat \beta_1 X_1\] Example: How does body mass index relate to physical activity?
In multiple linear regression there is more than one explanatory variable \[\hat Y = \hat \beta_0 + \hat \beta_1 X_1 + ... + \hat \beta_p X_p\] Example: How does systolic blood pressure relate to age and weight?
- \(\hat Y\) estimated mean of the response variable
- \(\hat \beta_0\) is the value of \(\hat Y\) when \(X_1=X_2=...=X_p=0\)
- \(\hat \beta_i\) denotes how much increase (or decrease) there is for \(\hat Y\) as the \(X_i\) variable increases by one unit given that the rest of variables remain constant, \(i=1,\ldots,p\)
In correlation analysis we assess the linear association between two variables when there is no clear response-explanatory relationship
Example: What is the correlation between arm length and leg length?
6.2 Correlation
The Pearson correlation \(r\) gives a measure of the linear relationship between two variables \(X\) and \(Y\).
Given a set of observations \((X_1, Y_1), (X_2,Y_2), \ldots, (X_n,Y_n)\), the correlation between \(X\) and \(Y\) is given by
\[r = \frac{1}{n-1} \sum_{i=1}^n \left(\frac{X_i-\bar X}{s_X}\right) \left(\frac{Y_i-\bar Y}{s_Y}\right),\] where \(\bar X\), \(\bar Y\), \(s_X\) and \(s_Y\) are the sample means and standard deviations for each variable.
Sample variances: \(s^2_X = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar X)^2,\ \ s^2_Y = \frac{1}{n-1} \sum_{i=1}^n (Y_i - \bar Y)^2\).
Sample covariance \(s_{XY} = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar X)(Y_i - \bar Y)\).
Sample correlation \(r_{XY} = \frac{s_{XY}}{s_X s_Y}\).
\[-1\leq r \leq 1\]
- \(r=-1\) is total negative correlation (increasing values in one variable correspond to decreasing values in the other variable)
- \(r=0\) is no correlation (there is not linear correlation between the variables)
- \(r=1\) is total positive correlation (increasing values in one variable correspond to increasing values in the other variable)
Correlation describes only the linear part of a relationship. It does not describe curved relationships.
Example
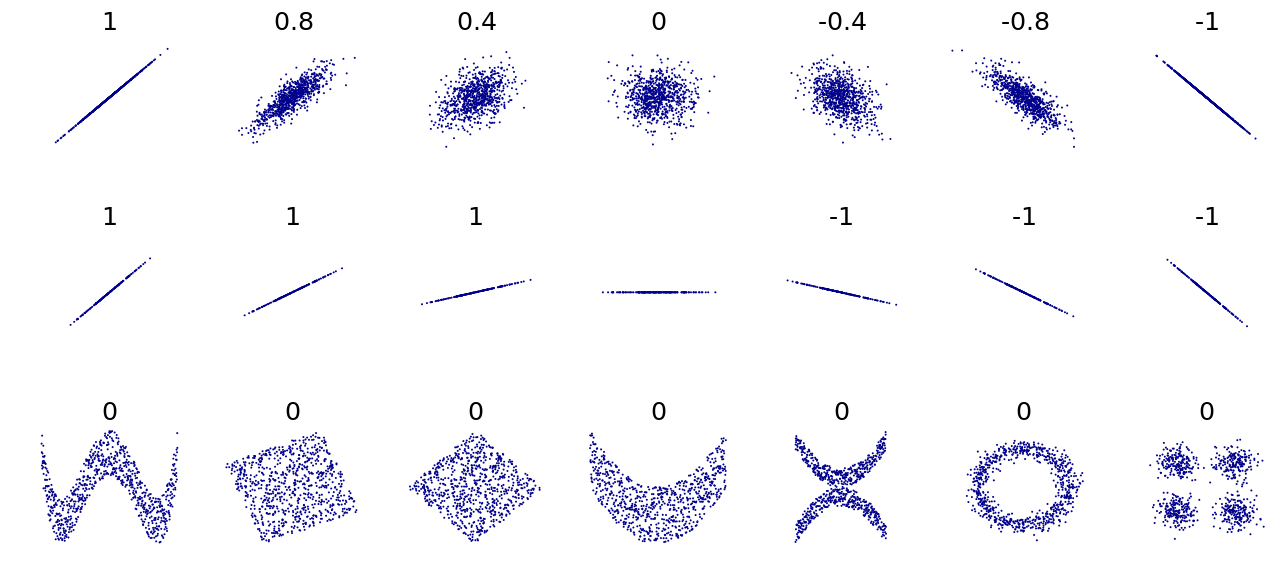
What is the correlation coefficients for these data sets?
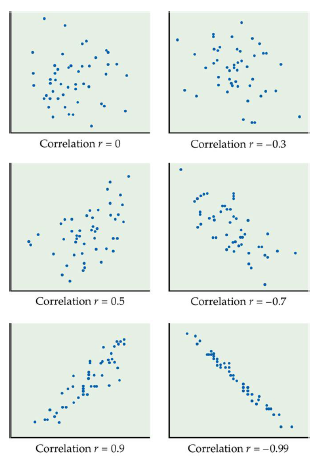
Solution
6.3 Linear regression
- Simple linear regression investigates if there is a linear relationship between a response variable and an explanatory variable
- \(Y\): response or dependent variable
- \(X\): explanatory or independent or predictor variable
- Simple linear regression fits a straight line in an explanatory variable \(X\) for the mean of a response variable \(Y\)
- The fitted line is the line closest to the points in the vertical direction. It is “closest” in the sense that the sum of squares of vertical distances is minimized.
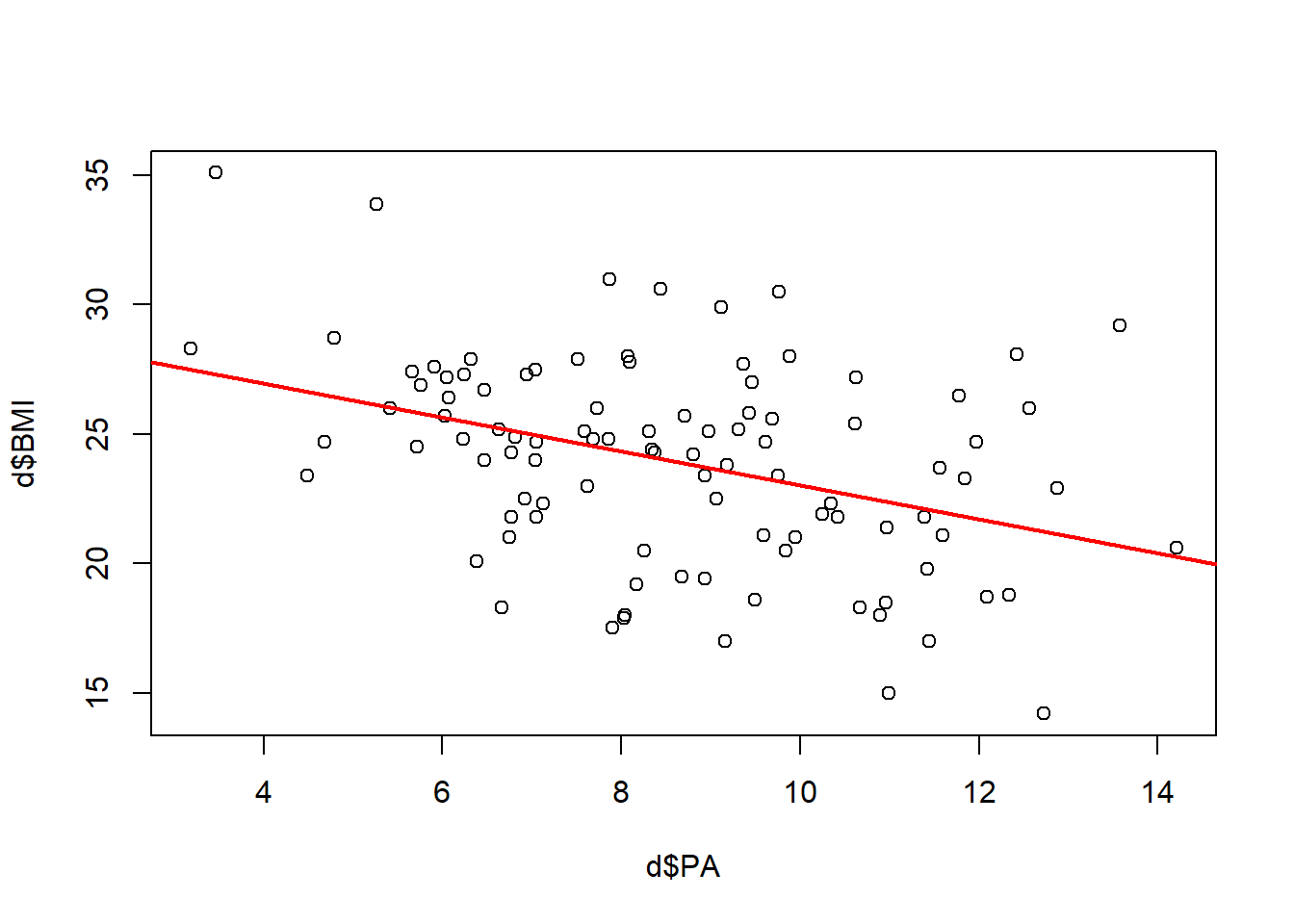
6.4 Residuals
- \(Y\): observed value of the response variable for a value of the explanatory variable equal to \(X\)
- \(\hat Y\): fitted or estimated mean of the response for a value of explanatory variable equal to \(X\)
- \(Y - \hat Y\): residual, difference between the observed and fitted values of the response for a value \(X\) of the explanatory variable
- Regression line is the line that minimizes the sum of squares of the residuals of all observations
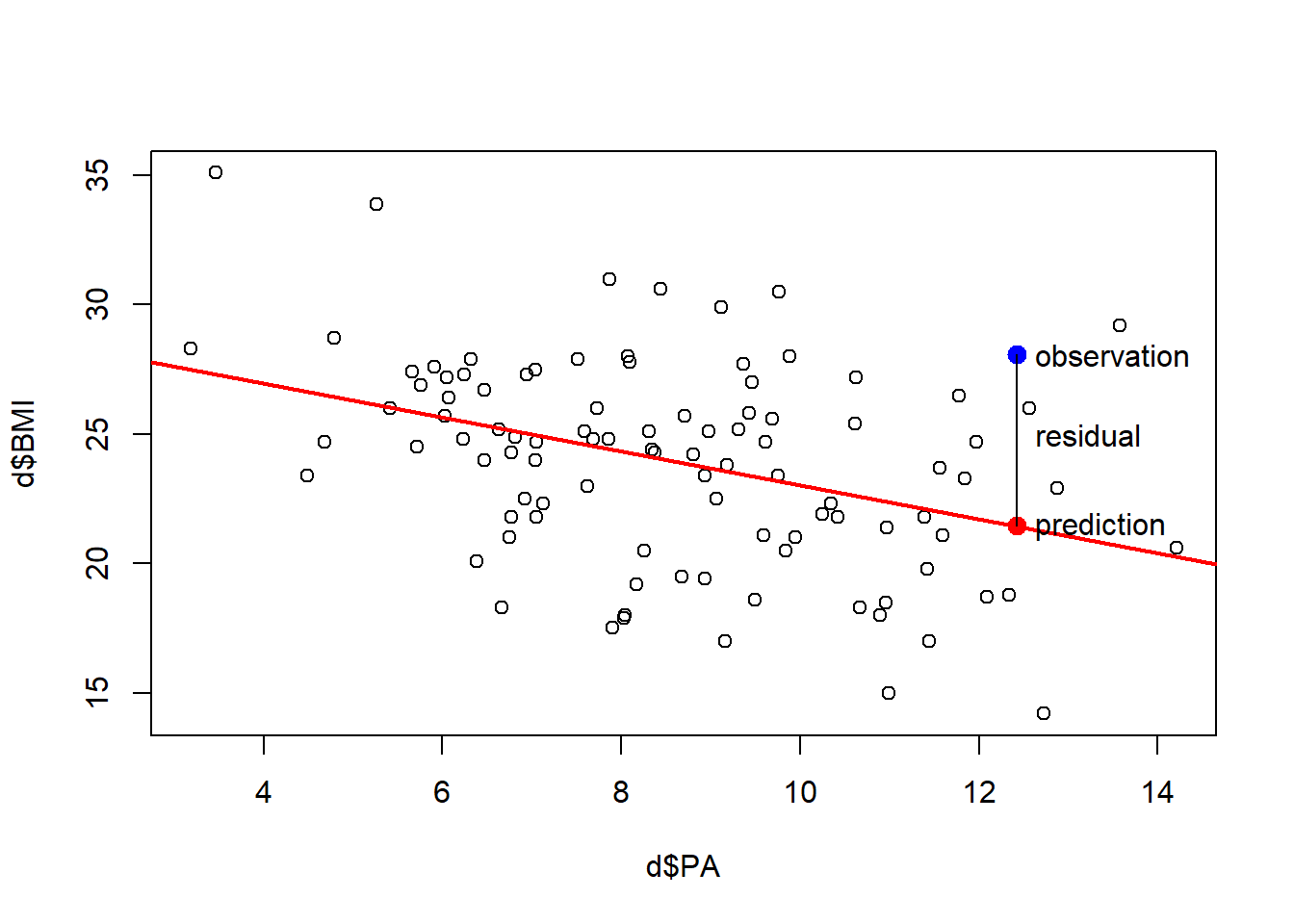
6.5 Regression line
\[Y_i = \beta_0 + \beta_1 X_{i} + \epsilon_i,\] where the error \(\epsilon_i \sim^{iid} N(0, \sigma^2), \ i = 1,\ldots,n\).
The equation of the least-squares regression line of \(Y\) on \(X\) is \[\hat Y = \hat \beta_0 + \hat \beta_1 X\]
\(\hat Y\) is the estimated mean of the response. \(\hat Y\) estimates the mean response for any value of \(X\) that we substitute in the fitted regression line
\(\hat \beta_0\) is the intercept of the fitted line. It is the value of \(\hat Y\) when \(X=0\).
\(\hat \beta_1\) is the slope of the fitted line. It tells how much increase (or decrease) there is for \(\hat Y\) as \(X\) increases by one unit
If \(\hat \beta_1>0\) \(\hat Y\) increases as \(X\) increases
If \(\hat \beta_1<0\) \(\hat Y\) decreases as \(X\) increases
The slope \(\hat \beta_1=r\frac{s_Y}{s_X} = \frac{s_{XY}}{s_X s_Y}\frac{s_Y}{s_X} = \frac{s_{XY}}{s^2_X} = \frac{\sum(X_i - \bar X)(Y_i-\bar Y)}{\sum (X_i - \bar X)^2}\) and the intercept \(\hat \beta_0 = \bar Y - \hat \beta_1 \bar X\)
Here \(r\) is the correlation which gives a measure of the linear relationship between \(X\) and \(Y\)
\[-1\leq r \leq 1\]
- \(r=-1\) is total negative correlation
- \(r=0\) is no correlation
- \(r=1\) is total positive correlation
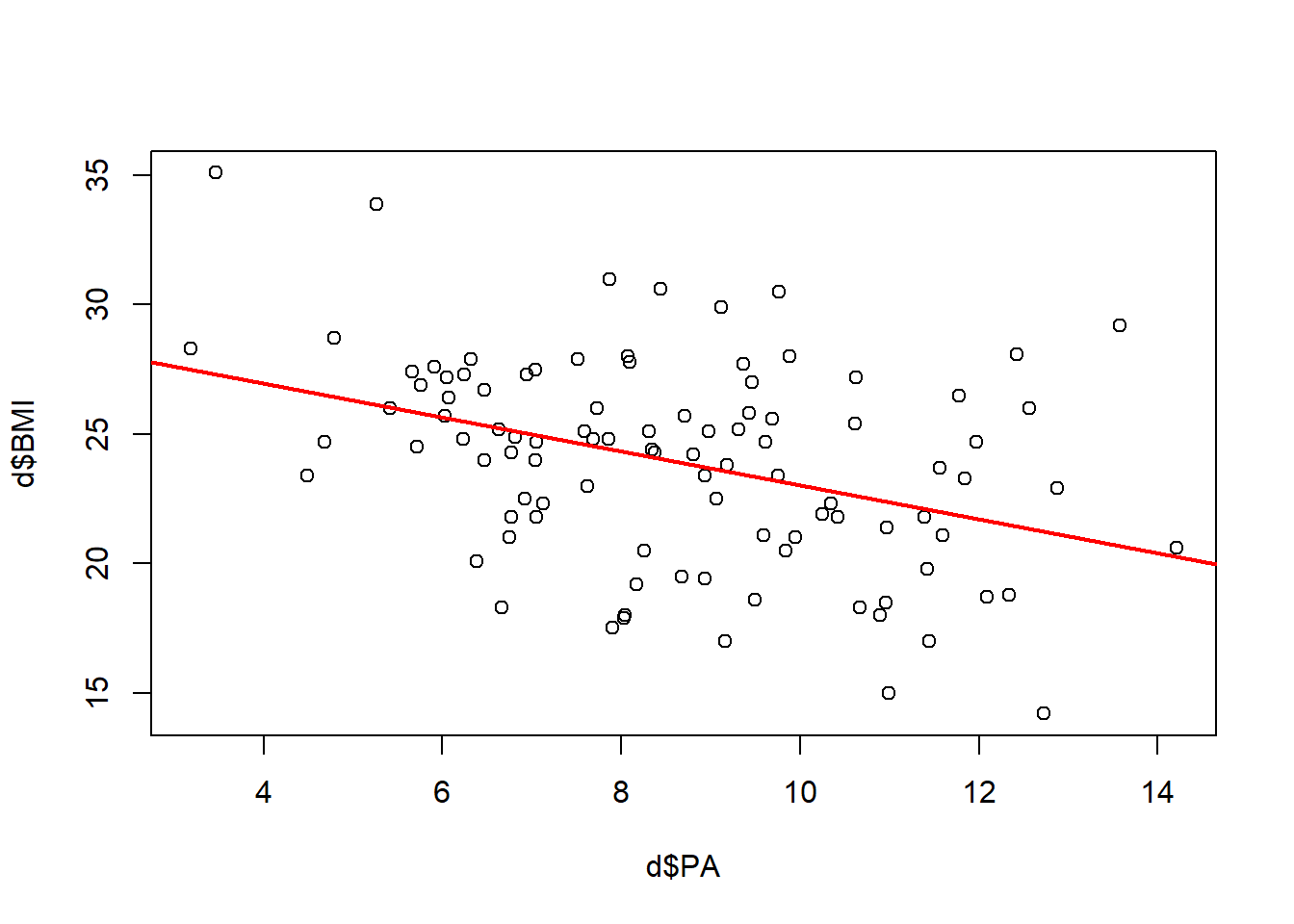
After fitting the model it is crucial to check whether the model assumptions are valid before performing inference. If there is any assumption violation, subsequent inferential procedures may be invalid. For example, we need to look at residuals. Are they randomly scattered so a straight line is a good model to fit?
6.6 Example. Simple Linear Regression
The Coast Starlight Amtrak train runs from Seattle to Los Angeles. The scatterplot below displays the distance between each stop (in miles) and the amount of time it takes to travel from one stop to another (in minutes).
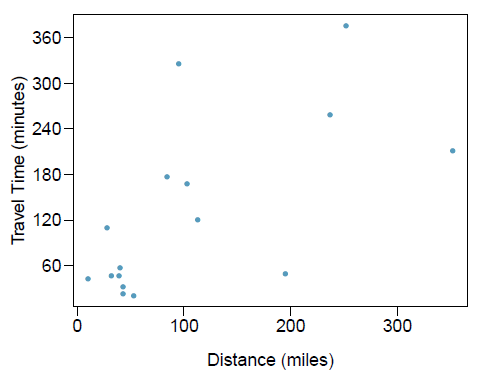
The mean travel time from one stop to the next on the Coast Starlight is 129 mins, with a standard deviation of 113 minutes. The mean distance traveled from one stop to the next is 108 miles with a standard deviation of 99 miles. The correlation between travel time and distance is 0.636.
- Write the equation of the regression line for predicting travel time.
- Interpret the slope and the intercept in this context.
- The distance between Santa Barbara and Los Angeles is 103 miles. Use the model to estimate the time it takes for the Starlight to travel between these two cities.
- It actually takes the Coast Starlight about 168 mins to travel from Santa Barbara to Los Angeles. Calculate the residual and explain the meaning of this residual value.
- Suppose Amtrak is considering adding a stop to the Coast Starlight 500 miles away from Los Angeles. Would it be appropriate to use this linear model to predict the travel time from Los Angeles to this point?
Solution
Travel time: \(\bar Y= 129\) minutes, \(s_Y = 113\) minutes.
Distance: \(\bar X = 108\) miles, \(s_X= 99\) miles.
Correlation between travel time and distance \(r = 0.63\).
First calculate the slope: \(\hat \beta_1 = r \times s_Y/s_X = 0.636 \times 113/99 = 0.726\). Next, make use of the fact that the regression line passes through the point \((\bar X, \bar Y)\): \(\bar Y = \hat \beta_0 + \hat \beta_1 \times \bar X\). Then, \(\hat \beta_0 = \bar Y - \hat \beta_1 \bar X = 129 - 0.726 \times 108 = 51\).
\(\widehat{\mbox{travel time}} = 51 + 0.726 \times \mbox{distance}\).\(\hat \beta_1\): For each additional mile in distance, the model predicts an additional 0.726 minutes in mean travel time.
\(\hat \beta_0\): When the distance traveled is 0 miles, the travel time is expected to be 51 minutes. It does not make sense to have a travel distance of 0 miles in this context. Here, the y-intercept serves only to adjust the height of the line and is meaningless by itself.\(\widehat{\mbox{travel time}} = 51 + 0.726 \times \mbox{distance} = 51+0.726 \times 103 \approx 126\) minutes.
(Note: we should be cautious in our predictions with this model since we have not yet evaluated whether it is a well-fit model).\(e_i = Y_i - \hat Y_i = 168-126=42\) minutes. A positive residual means that the model underestimates the travel time.
I would not be appropriate since this calculation would require extrapolation.