d <- read.table("data/pabmi.txt", header = TRUE)9 Example code SLR
9.1 BMI and physical activity
- Researchers are interested in the relationship between physical activity (PA) measured with a pedometer and body mass index (BMI)
- A sample of 100 female undergraduate students were selected. Students wore a pedometer for a week and the average steps per day (in thousands) was recorded. BMI (kg/m\(^2\)) was also recorded.
- Is there a statistically significant linear relationship between physical activity and BMI? If so, what is the nature of the relationship?
Read data
First rows of data
head(d) SUBJECT PA BMI
1 1 10.992 15.0
2 2 6.753 21.0
3 3 12.423 28.1
4 4 6.249 27.3
5 5 11.595 21.1
6 6 14.209 20.6Summary data
summary(d) SUBJECT PA BMI
Min. : 1.00 Min. : 3.186 Min. :14.20
1st Qu.: 25.75 1st Qu.: 6.803 1st Qu.:21.10
Median : 50.50 Median : 8.409 Median :24.45
Mean : 50.50 Mean : 8.614 Mean :23.94
3rd Qu.: 75.25 3rd Qu.:10.274 3rd Qu.:26.75
Max. :100.00 Max. :14.209 Max. :35.10 Scatterplot of BMI versus PA
plot(d$PA, d$BMI)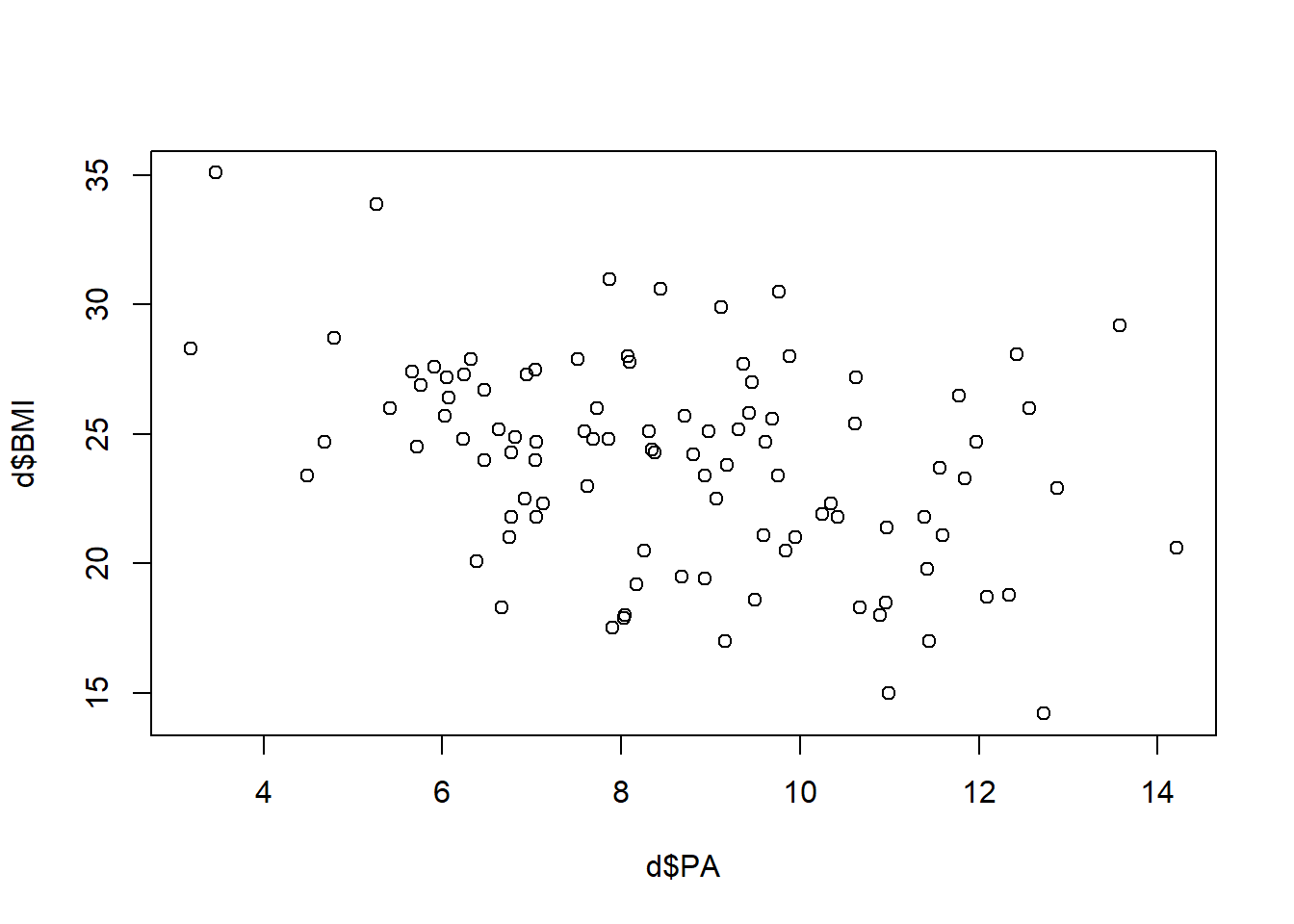
There is a lot of variation but does it look like there is a linear trend? Could the average BMI be a straight line in PA?
9.2 Coefficients of the regression line
res <- lm(BMI ~ PA, data = d)
summary(res)
Call:
lm(formula = BMI ~ PA, data = d)
Residuals:
Min 1Q Median 3Q Max
-7.3819 -2.5636 0.2062 1.9820 8.5078
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.5782 1.4120 20.948 < 2e-16 ***
PA -0.6547 0.1583 -4.135 7.5e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.655 on 98 degrees of freedom
Multiple R-squared: 0.1485, Adjusted R-squared: 0.1399
F-statistic: 17.1 on 1 and 98 DF, p-value: 7.503e-05- \(\hat Y = \hat \beta_0 + \hat \beta_1 X\)
- \(\widehat{BMI} = 29.58 + (- 0.65) PA\)
- \(\hat \beta_0= 29.58\) is the mean value of BMI when \(PA=0\)
- \(\hat \beta_1= - 0.65\) means the mean value of BMI decreases by 0.65 for every unit increase in PA
9.3 Tests for coefficients. t test
The most important test is whether the slope is 0 or not. If the slope is 0, then there is no linear relationship. Test null hypothesis ‘response variable \(Y\) is not linearly related to variable \(X\)’ versus alternative hypothesis ‘\(Y\) is linearly related to \(X\)’.
\(H_0: \beta_1 =0\)
\(H_1: \beta_1 \neq 0\)Test statistic: t-value = estimate of the coefficient / SE of coefficient
\[T = \frac{\hat \beta_1 - 0}{SE_{\hat \beta_1}}\]
- Distribution: t distribution with degrees of freedom = number of observations - 2 (because we are fitting an intercept and a slope)
\[T \sim t(n-2)\]
- p-value: probability of obtaining a test statistic as extreme or more extreme than the observed, assuming the null is true.
\(H_1: \beta_1 \neq 0\). p-value is \(P(T\geq |t|)\)
summary(res)$coefficients Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.5782471 1.4119783 20.948089 5.706905e-38
PA -0.6546858 0.1583361 -4.134784 7.503032e-05In the example p-value=7.503032e-05. There is strong evidence to suggest slope is not zero. There is strong evidence to suggest PA and BMI are linearly related.
Output also gives test for intercept. This tests the null hypothesis the intercept is 0 versus the alternative hypothesis the intercept is not 0. Usually we are not interested in this test.
9.4 Confidence interval for the slope \(\beta_1\)
A \((c)\times 100\)% (or \((1-\alpha)\times 100\)%) confidence interval for the slope \(\beta_1\) is \[\hat \beta_1 \pm t^* \times SE_{\hat \beta_1}\]
\(t^*\) is the value on the \(t(n-2)\) density curve with area \(c\) between the critical points \(-t^*\) and \(t^*\). Equivalently, \(t^*\) is the value such that \(\alpha/2\) of the probability in the \(t(n-2)\) distribution is below \(t^*\).
9.5 ANOVA. F test
summary(res)
Call:
lm(formula = BMI ~ PA, data = d)
Residuals:
Min 1Q Median 3Q Max
-7.3819 -2.5636 0.2062 1.9820 8.5078
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.5782 1.4120 20.948 < 2e-16 ***
PA -0.6547 0.1583 -4.135 7.5e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.655 on 98 degrees of freedom
Multiple R-squared: 0.1485, Adjusted R-squared: 0.1399
F-statistic: 17.1 on 1 and 98 DF, p-value: 7.503e-05Test null hypothesis ‘none of the explanatory variables are useful predictors of the response variable’ versus alternative hypothesis ‘at least one of the explanatory variables is related to the response variable’
\(H_0\): \(\beta_{1} =\beta_{2}=...=\beta_{p}\) = 0 (all coefficients are 0)
\(H_1\): at least one of \(\beta_1\), \(\beta_2\), \(\dots\), \(\beta_p \neq\) 0 (not all coefficients are 0)
- In simple linear regression, this is doing the same test as the t test. Test null hypothesis ‘response variable \(Y\) is not linearly related to variable \(X\)’ versus alternative hypothesis ‘\(Y\) is linearly related to \(X\)’.
- The p-value is the same.
- We will look at ANOVA in multiple regression.
9.6 R\(^2\) in simple linear regression
- R\(^2\) (R-squared or coefficient of determination) is the proportion of variation of the response variable \(Y\) that is explained by the model.
\[R^2 = \frac{\mbox{variability explained by the model}}{\mbox{total variability}} = \frac{\sum_{i=1}^n (\hat Y_i - \bar Y)^2}{\sum_{i=1}^n (Y_i - \bar Y)^2}\]
or equivalently
\[R^2 = 1 - \frac{\mbox{variability in residuals}}{\mbox{total variability}} = 1 - \frac{\sum_{i=1}^n (Y_i - \hat Y_i)^2}{\sum_{i=1}^n (Y_i - \bar Y)^2}\]
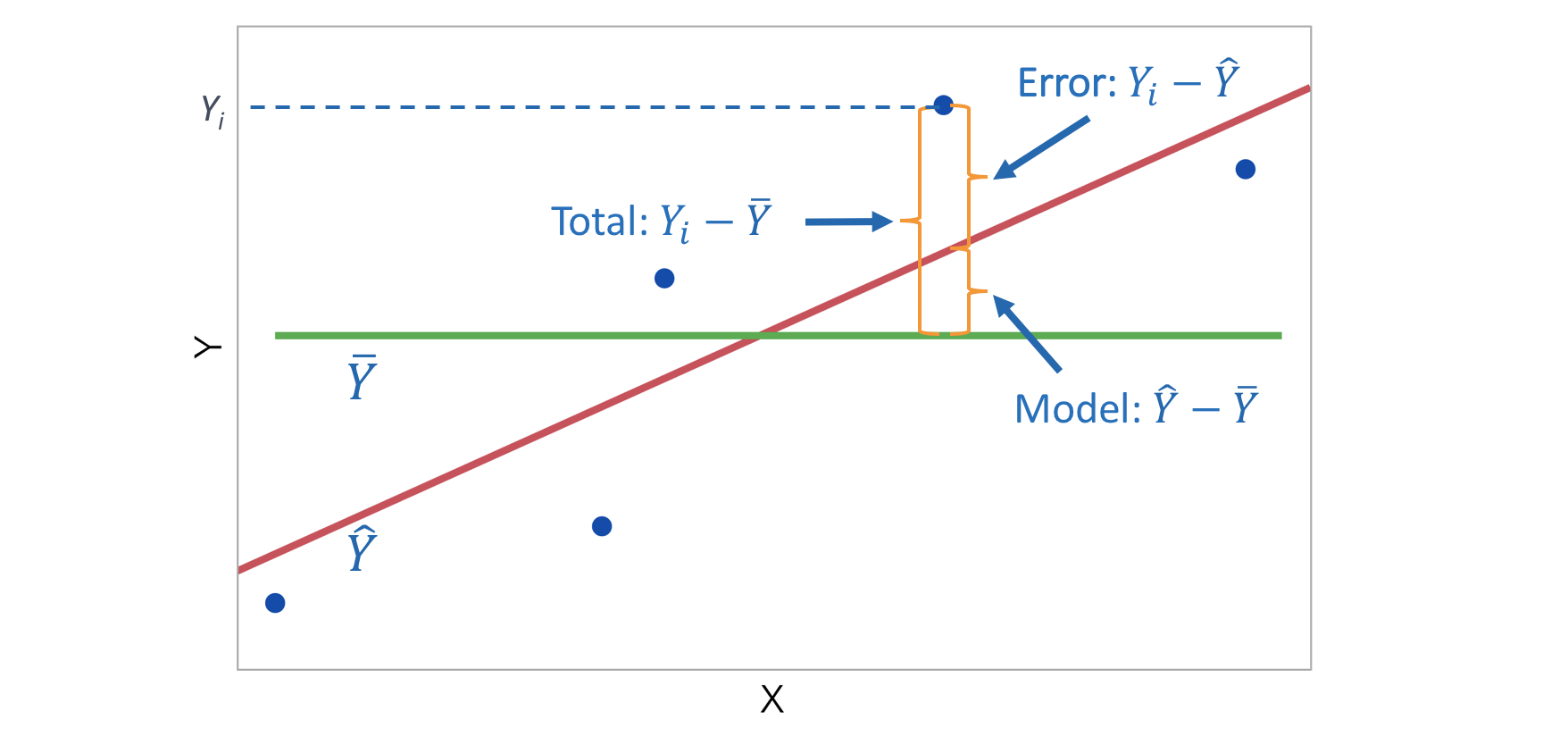
R\(^2\) measures how successfully the regression explains the response.
If the data lie exactly on the regression line then R\(^2\) = 1.
If the data are randomly scattered or in a horizontal line then R\(^2\) = 0.
For simple linear regression, R\(^2\) is equal to the square of the correlation between response variable \(Y\) and explanatory variable \(X\). \[R^2 = r^2\]
Remember the correlation \(r\) gives a measure of the linear relationship between \(X\) and \(Y\)
\[-1\leq r \leq 1\]
- \(r=-1\) is total negative correlation
- \(r=0\) is no correlation
- \(r=1\) is total positive correlation
\(R^2\) will increase as more explanatory variables are added to a regression model. We look at R\(^2\)(adj).
R\(^2\)(adj) or Adjusted R-squared is the proportion of variation of the response variable explained by the fitted model adjusting for the number of parameters.
- In the example R\(^2\)(adj)=13.99%. The model explains about 14% of the variation of BMI adjusting for the number of parameters.
summary(res)$adj.r.squared[1] 0.13985189.7 Estimation and prediction
9.7.1 Estimation and prediction
The regression equation can be used to estimate the mean response or to predict a new response for particular values of the explanatory variable.
When PA is 10, the estimated mean of BMI is \(\widehat{BMI} = \hat \beta_0 + \hat \beta_1 \times 10 = 29.5782 - 0.6547 \times 10 = 23.03\).
When PA is 10, the predicted BMI of a new individual is also \(\widehat{BMI} = \hat \beta_0 + \hat \beta_1 \times 10 = 29.5782 - 0.6547 \times 10 = 23.03\).
Extrapolation occurs when we estimate the mean response or predict a new response for values of the explanatory variables which are not in the range of the data used to determine the estimated regression equation. In general, this is not a good thing to do.
When PA is 50, the estimated mean of BMI is \(\widehat{BMI} = \hat \beta_0 + \hat \beta_1 \times 50 = 29.5782 - 0.6547 \times 50 = -3.15\).
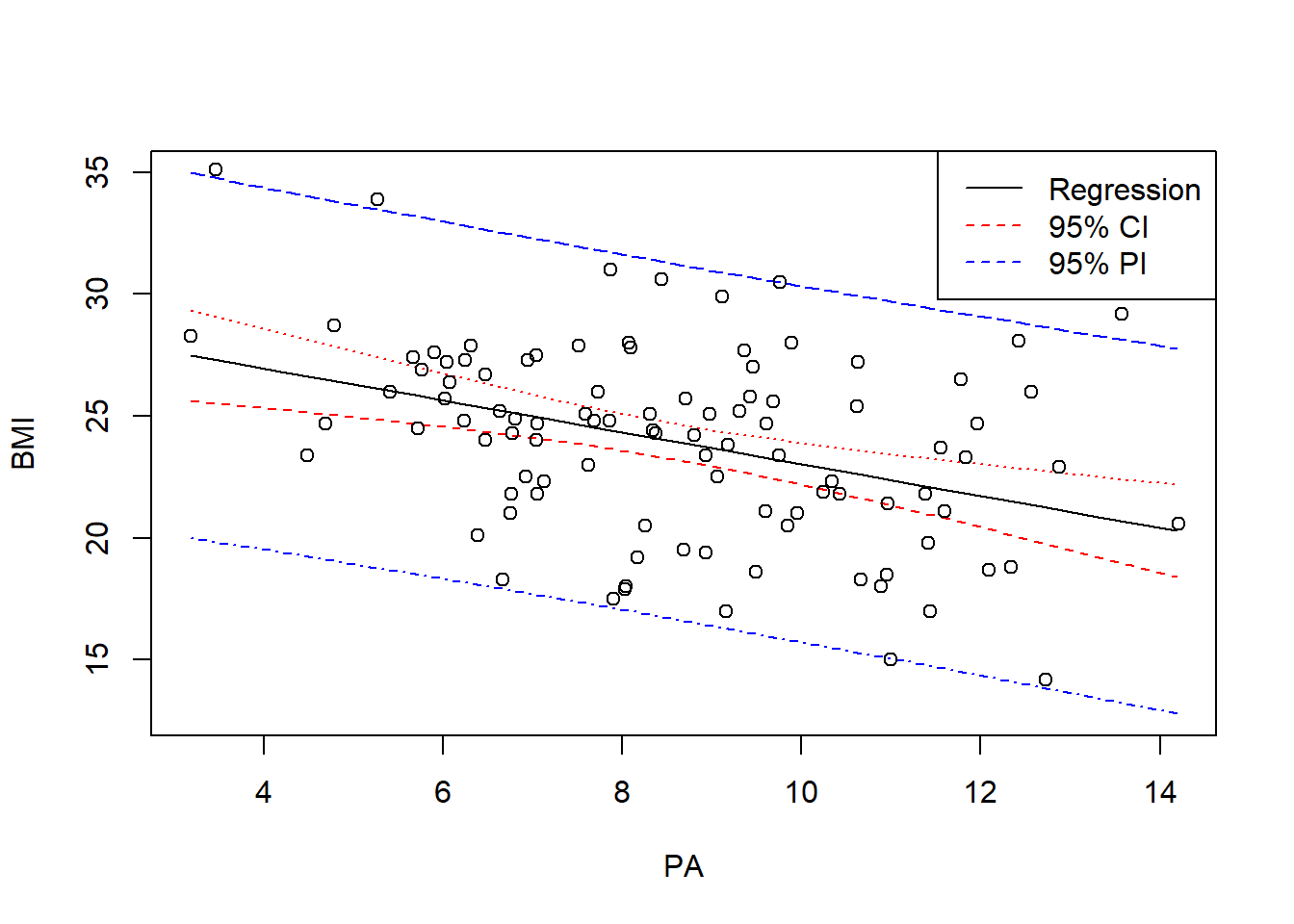
9.7.2 Confidence and prediction intervals
A confidence interval is an interval estimate for the mean response for particular values of the explanatory variables
We can calculate the 95% CI as \(\widehat{Y} \pm t^* \times SE(\widehat{Y})\) where \(t^*\) is the value such that \(\alpha/2\) probability on the t(n-2) distribution is below \(t^*\).
In R, we can calculate the 95% CI with the predict() function and the option interval = "confidence".
new <- data.frame(PA = 10)
predict(lm(BMI ~ PA, data = d), new, interval = "confidence", se.fit = TRUE)$fit
fit lwr upr
1 23.03139 22.18533 23.87744
$se.fit
[1] 0.4263387
$df
[1] 98
$residual.scale
[1] 3.654883c(23.03139 + qt(0.05/2, 98)*0.4263387,
23.03139 - qt(0.05/2, 98)*0.4263387)[1] 22.18533 23.87745A prediction interval is an interval estimate for an individual value of the response for particular values of the explanatory variables
We can calculate the 95% PI as \(\widehat{Y}_{new} \pm t^* \times \sqrt{MSE + [SE(\widehat{Y})]^2}\) where \(t^*\) is the value such that \(\alpha/2\) probability on the t(n-2) distribution is below \(t^*\). The Residual standard error and $residual.scale in the R output is equal to \(\sqrt{MSE}\).
In R, we can calculate the 95% CI with the predict() function and the option interval = "prediction".
predict(lm(BMI ~ PA, data = d), new, interval = "prediction", se.fit = TRUE)$fit
fit lwr upr
1 23.03139 15.72921 30.33357
$se.fit
[1] 0.4263387
$df
[1] 98
$residual.scale
[1] 3.654883c(23.03139 + qt(0.05/2, 98)*sqrt(3.654883^2 + 0.4263387^2),
23.03139 - qt(0.05/2, 98)*sqrt(3.654883^2 + 0.4263387^2))[1] 15.72921 30.33357- Prediction intervals are wider than confidence intervals because there is more uncertainty in predicting an individual value of the response variable than in estimating the mean of the response variable
- The formula for the prediction interval has the extra MSE term. A confidence interval for the mean response will always be narrower than the corresponding prediction interval for a new observation.
- The width of the intervals reflects the amount of information over the range of possible \(X\) values. We are more certain of predictions at the center of the data than at the edges. Both intervals are narrowest at the mean of the explanatory variable.