35 LM1
35.1 Regression through the origin
Consider a simple linear regression that goes through the origin:
\[Y_i = \beta X_i + \epsilon_i,\]
where \(\epsilon_i \sim^{iid} N(0, \sigma^2)\), for \(i=1,2,\ldots,n\).
Write down the expression for the sum of squared residuals and solve for the least squares estimator of the slope, \(\hat \beta\).
What is the mean of \(\hat \beta\)? Is this estimator unbiased?
What is the variance of \(\hat \beta\)?
Construct a 95% confidence interval for \(\beta\) based on the sampling distribution of \(\hat \beta\) assuming that \(\sigma^2\) is known.
Regression through the origin. Solutions
\[\frac{dSSE}{d\beta}=\frac{d(\sum(Y_i - \beta X_i)^2)}{d\beta} = -2 \sum [X_i(Y_i-\beta X_i)]=0\]
\[\hat \beta = \frac{\sum(X_i Y_i)}{\sum X_i^2}\]
\[E[\hat \beta] = E\left[\frac{\sum(X_i Y_i)}{\sum X_i^2}\right]=\frac{\sum(X_i E(Y_i))}{\sum X_i^2}= \frac{\sum(X_i \beta X_i)}{\sum X_i^2} = \frac{\beta \sum X_i^2}{\sum X_i^2}=\beta\]
\[Var[\hat \beta] = Var\left[\frac{\sum(X_i Y_i)}{\sum X_i^2}\right]=\frac{\sum(X_i^2 Var(Y_i))}{(\sum X_i^2)^2}= \frac{\sum(X_i^2 \sigma^2)}{(\sum X_i^2)^2} = \frac{\sigma^2}{\sum X_i^2}\]
Since \(\sigma^2\) is known, then everything will be Normal, and standard deviation can be left in terms of \(\sigma\) and does not need to be estimated.
\[\hat \beta \pm z^*_{1-\alpha/2} se(\hat \beta) = \frac{\sum X_i Y_i}{\sum X_i^2} \pm 1.96 \frac{\sigma}{\sqrt{\sum X_i^2}}\]
35.2 \(F\) and \(R^2\)
\(F\) and \(R^2\) are related. Find the expression.
\(F\) and \(R^2\). Solutions
Solution
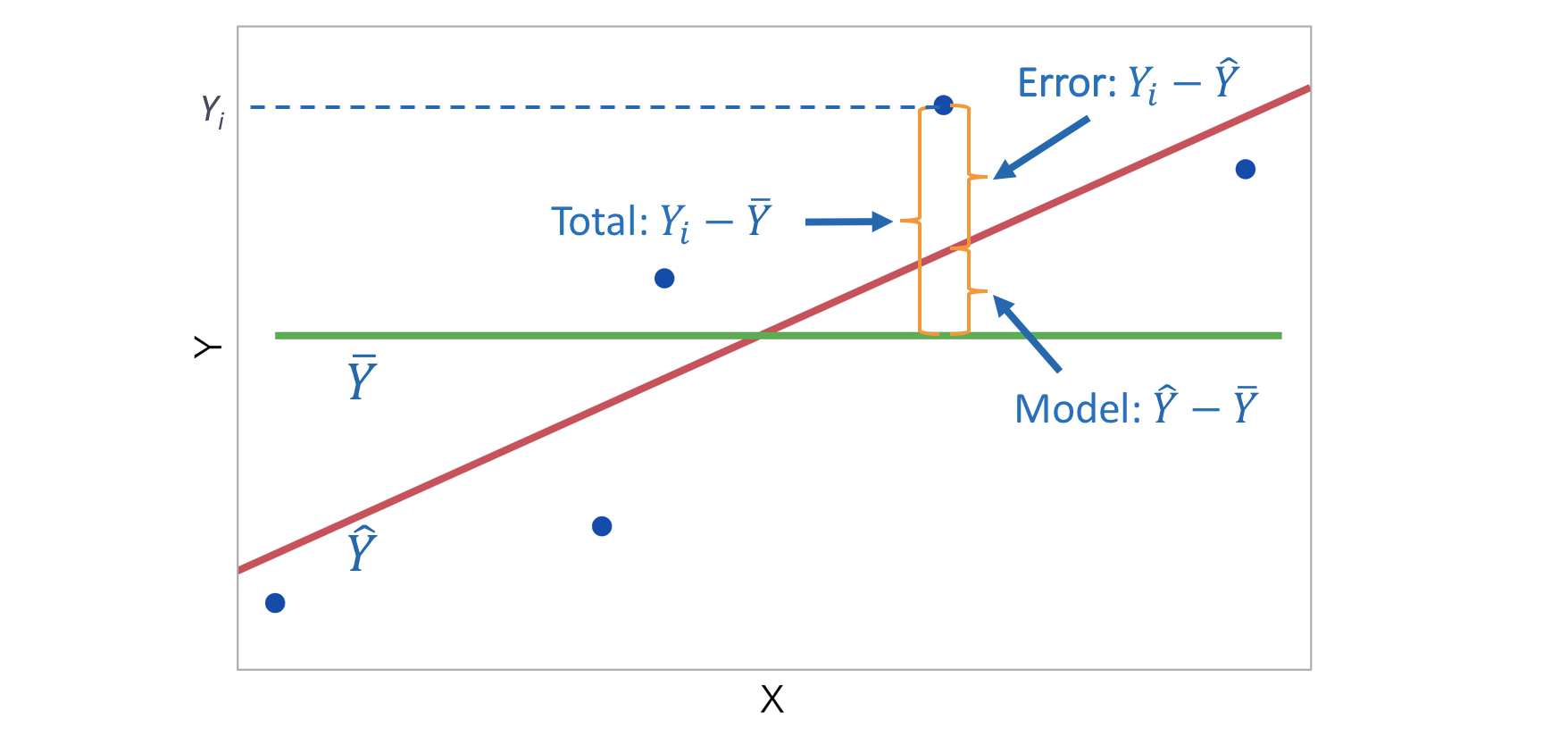
\[R^2 = \frac{SSM}{SST} = \frac{\sum_{i=1}^n (\hat y_i - \bar y)^2}{\sum_{i=1}^n ( y_i - \bar y)^2} \ \ \ \mbox{(proportion of variability explained by the model)}\]
\[R^2 = 1 - \frac{SSE}{SST} = 1 - \frac{\sum_{i=1}^n ( y_i - \hat y_i)^2}{\sum_{i=1}^n ( y_i - \bar y)^2} \ \ \ \mbox{(1 - proportion of variability not explained by the model)}\]
\[F = \frac{MSM}{MSE} = \frac{\sum_{i=1}^n (\hat y_i - \bar y)^2/p}{\sum_{i=1}^n ( y_i - \hat y_i)^2/(n-p-1)} = \frac{\frac{\sum_{i=1}^n (\hat y_i - \bar y)^2}{\sum_{i=1}^n ( y_i - \bar y)^2}/p} {\frac{\sum_{i=1}^n (y_i - \hat y_i)^2}{\sum_{i=1}^n ( y_i - \bar y)^2}/(n-p-1)} = \frac{R^2/p}{(1-R^2)/(n-p-1)}\]